【题目】已知:如图,l∥m,等边△ABC的顶点B在直线m上,边BC与直线m所夹锐角为20°,则∠α的度数为( )
A.60°![]()
B.45°
C.40°
D.30°
参考答案:
【答案】C
【解析】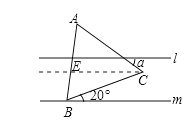 过C作CE∥直线m
过C作CE∥直线m
∵l∥m,
∴l∥m∥CE,
∴∠ACE=∠α,∠BCE=∠CBF=20°,
∵等边△ABC,
∴∠ACB=60°,
∴∠α+∠CBF=∠ACB=60°,
∴∠α=40°.
故选C.
【考点精析】认真审题,首先需要了解平行线的性质(两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补),还要掌握三角形的外角(三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线DE经过点A.
(1)写出∠B的内错角是 ,同旁内角是 .
(2)若∠EAC=∠C,AC平分∠BAE,∠B=44°,求∠C的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )

A.45°
B.54°
C.40°
D.50° -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明过程:
如图所示,直线AD与AB,CD分别相交于点A,D,与EC,BF分别相交于点H,G,已知∠1=∠2,∠B=∠C.
求证:∠A=∠D.
证明:∵∠1=∠2,(已知)∠2=∠AGB( )
∴∠1= ( )
∴EC∥BF( )
∴∠B=∠AEC( )
又∵∠B=∠C(已知)
∴∠AEC= ( )
∴ ( )
∴∠A=∠D( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,三角形ABC的位置如图所示,把三角形ABC平移后,三角形ABC内任意点P(x,y)对应点为P′(x+3,y﹣4).
(1)画出平移后的图形;
(2)三角形ABC是经过怎样平移后得到三角形
 ?
?(3)在三角形ABC平移到
 的过程中,线段AB扫过的面积为 .
的过程中,线段AB扫过的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两直线L1:y=k1x+b1 , L2:y=k2x+b2 , 若L1⊥L2 , 则有k1k2=﹣1.
(1)应用:已知y=2x+1与y=kx﹣1垂直,求k;
(2)直线经过A(2,3),且与y= x+3垂直,求解析式.
x+3垂直,求解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, 是
是 边上一点,将
边上一点,将 绕着点
绕着点 逆时针旋转至
逆时针旋转至 ,连接
,连接 .
.
(1)如图1,连接
 ,当
,当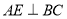 时,
时,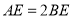 ,若
,若 ,
, ,
, ,求线段
,求线段 的长.
的长.(2)如图2,连接
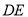 交
交 于点
于点 ,若
,若 ,点
,点 为
为 中点,求证:
中点,求证: .
.
相关试题

