Question

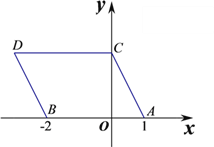
【题目】如图，在平面直角坐标系中，点的坐标分别为(1，0)、(-2，0)，现同时将点分别向上平移2个单位，再向左平移1个单位，分别得到点的对应点，连接、、.

（1）若在轴上存在点,连接，使S△ABM =S□ABDC，求出点的坐标；

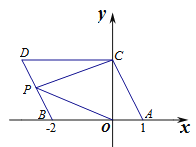
（2）若点在线段上运动，连接，求S=S△PCD+S△POB的取值范围；

（3）若在直线上运动，请直接写出的数量关系.

Answer 1

【答案】（1）(0，4)或(0，-4)；（2）；（3）答案见解析

【解析】（1）先根据S△ABM =S□ABDC，得出△ABM的高为4，再根据三角形面积公式得到M点的坐标；

（2）先计算出S梯形OBDC=5，再讨论：当点P运动到点B时，S△POC的最小值=2，当点P运动到点D时，S△POC的最大值=3，即可判断S=S△PCD+S△POB的取值范围的取值范围；

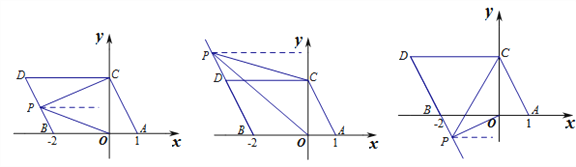
（3）分类讨论：当点P在BD上，如图1，作PE∥CD，根据平行线的性质得CD∥PE∥AB，则∠DCP=∠EPC，∠BOP=∠EPO，易得∠DCP+∠BOP=∠EPC+∠EPO=∠CPO；

当点P在线段BD的延长线上时，如图2，同样有∠DCP=∠EPC，∠BOP=∠EPO，由于∠EPO-∠EPC=∠BOP-∠DCP，于是∠BOP-∠DCP=∠CPO；同理可得当点P在线段DB的延长线上时，∠DCP-∠BOP=∠CPO．

解：（1）由题意，得C（0，2）

∴□ABDC的高为2

若S△ABM =S□ABDC，则△ABM的高为4

又∵点M是y轴上一点

∴点M的坐标为(0，4)或(0，-4)

（2）∵B（-2，0），O（0，0）

∴OB=2

由题意，得C（0，2），D（-3，2）

∴OC=2，CD=3

∴S梯形OBDC=

点在线段上运动，

当点运动到端点B时，△PCO的面积最小，为

当点运动到端点D时，△PCO的面积最大，为

∴S=S△PCD+S△POB= S梯形OBDC－S△PCO=5－S△PCO

∴S的最大值为5－2=3，最小值为5－3=2

故S的取值范围是：

（3）如图：

当点在线段上运动时，

当点在射线上运动时，

当点在射线上运动时，