【题目】如图,△ABC中,AB=AC,AD⊥BC于点D,AE是∠BAC外角平分线,BE⊥AE,连接DE.

(1)求证:DA⊥AE;
(2)求证:四边形DCAE是平行四边形.
参考答案:
【答案】见解析
【解析】
试题分析:(1)根据三线合一定理证明AD平分∠BAC,然后根据AE是∠BAC外角平分线,即可证得∠DAE=90°,即可证得DA⊥AE;
(2)根据平行四边形的定义即可证得.
证明:(1)∵AB=AC,AD⊥BC于点D,
∴∠CAD=∠BAD,即∠BAD=![]() ∠BAC,
∠BAC,
又∵AE是∠BAC外角平分线,即∠BAE=![]() ∠BAF,
∠BAF,
∴∠DAE=∠BAD+∠BAE=![]() (∠BAC+∠BAF)=90°,
(∠BAC+∠BAF)=90°,
∴DA⊥AE;
(2)∵AD⊥BC,DA⊥AE,
∴BD∥AE,即CD∥AE.
∵BE⊥AE,DA⊥AE,
∴BE∥AD,
∴四边形BDAE是平行四边形.
∴BD=AE,
又∵AB=AC,AD⊥BC,
∴BD=CD,
又∵CD∥AE,
∴四边形DCAE是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A. 0既不是正数,也不是负数 B. ﹣1是最大的负整数
C. ﹣a一定是负数 D. 倒数等于它本身的数有1和﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,M为PQ中点.

(1)求证:△ADP∽△ABQ;
(2)若AD=10,AB=20,点P在边CD上运动,设DP=x,BM2=y,求y与x的函数关系式,并求线段BM的最小值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.

(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6
 ,AF=4
,AF=4 ,求AE的长.
,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若AB∥CD,在下列三种情况下探究∠APC与∠PAB,∠PCD的数量关系.
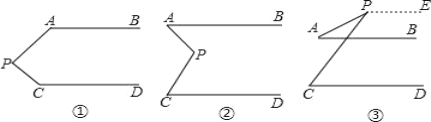
(1)图①中,∠APC+∠PAB+∠PCD= ;
(2)图②中, ;
(3)图③中,写出∠APC与∠PAB,∠PCD的三者数量关系,并说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列几种形状的瓷砖中,只用一种不能够铺满地面的是( )
A. 正三角形; B. 正四边形; C. 正五边形; D. 正六边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.8a﹣a=8
B.(﹣a)4=a4
C.a3a2=a6
D.(a﹣b)2=a2﹣b2
相关试题

