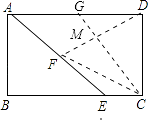
【题目】如图,在矩形ABCD中,AB=2 ![]() ,AD=4,点E是BC边上一个动点,连接AE,作DF⊥AE于点F,当BE的长为时,△CDF是等腰三角形.
,AD=4,点E是BC边上一个动点,连接AE,作DF⊥AE于点F,当BE的长为时,△CDF是等腰三角形. 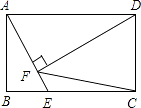
参考答案:
【答案】2或2 ![]() 或4﹣2
或4﹣2 ![]()
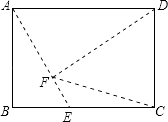
【解析】解:①CF=CD时,过点C作CM⊥DF,垂足为点M,
则CM∥AE,DM=MF,
延长CM交AD于点G,
∴AG=GD=2,
∴CE=2,
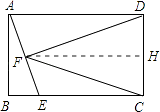
∴当BE=2时,△CDF是等腰三角形;②DF=DC时,则DF=DC=AB=2 ![]() ,
,
∵DF⊥AE,AD=2,
∴∠DAE=45°,
则BE=2 ![]() ,
,
∴当BE=2 ![]() 时,△CDF是等腰三角形;③FD=FC时,则点F在CD的垂直平分线上,故F为AE中点.
时,△CDF是等腰三角形;③FD=FC时,则点F在CD的垂直平分线上,故F为AE中点.
∵AB=2 ![]() ,BE=x,
,BE=x,
∴AE= ![]() ,
,
AF= ![]() ,
,
∵△ADF∽△EAB,
∴ ![]() ,即
,即 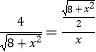 ,
,
解得:x=4﹣2 ![]() 或x=4+2
或x=4+2 ![]() (舍去);
(舍去);
∴当BE=4﹣2 ![]() 时,△CDF是等腰三角形.
时,△CDF是等腰三角形.
综上,当BE=2或2 ![]() 或4﹣2
或4﹣2 ![]() 时,△CDF是等腰三角形.
时,△CDF是等腰三角形.
所以答案是:2或2 ![]() 或4﹣2
或4﹣2 ![]() .
.
【考点精析】通过灵活运用等腰三角形的判定和矩形的性质,掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等;矩形的四个角都是直角,矩形的对角线相等即可以解答此题.
-
科目: 来源: 题型:
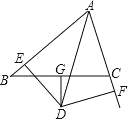
查看答案和解析>>【题目】如图,G 为 BC 的中点,且 DG⊥BC,DE⊥AB 于 E,DF⊥AC 于 F, BE=CF.
(1)求证:AD 是∠BAC 的平分线;
(2)如果 AB=8,AC=6,求 AE 的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)解方程: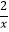 ﹣
﹣ 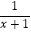 =0;
=0;
(2)解不等式组: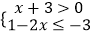 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,CD⊥AB于D点,M,N是AC,BC上的动点,且∠MDN=90°,下列结论:①AM=CN;②四边形MDNC的面积为定值;③AM2+BN2=MN2;④NM平分∠CND.其中正确的是 ( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料后解决问题:
小明遇到下面一个问题:
计算(2+1)(22+1)(24+1)(28+1).
经过观察,小明发现如果将原式进行适当的变形后可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:(2+1)(22+1)(24+1)(28+1)
=(2+1)(2﹣1)(22+1)(24+1)(28+1)
=(22﹣1)(22+1)(24+1)(28+1)
=(24﹣1)(24+1)(28+1)
=(28﹣1)(28+1)
=216﹣1
请你根据小明解决问题的方法,试着解决以下的问题:
(1)(2+1)(22+1)(24+1)(28+1)(216+1)=_____.
(2)(3+1)(32+1)(34+1)(38+1)(316+1)=_____.
(3)化简:(m+n)(m2+n2)(m4+n4)(m8+n8)(m16+n16).
-
科目: 来源: 题型:
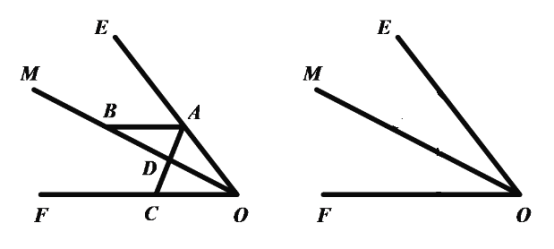
查看答案和解析>>【题目】如图
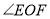 ,
,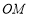 平分
平分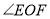 ,点
,点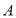 、
、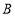 、
、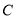 分别是射线
分别是射线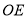 、
、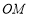 、
、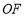 上的点(点
上的点(点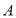 、
、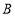 、
、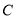 不与点
不与点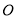 重合),联结
重合),联结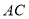 ,交射线
,交射线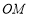 与点
与点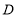 .
.
(1)如果
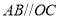 ,
,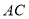 平分
平分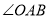 ,试判断
,试判断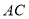 与射线
与射线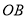 的位置关系,试说明理由;
的位置关系,试说明理由;(2)如果
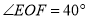 ,
,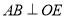 ,垂足为点
,垂足为点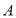 ,
,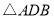 中有两个相等的角,请直接写出
中有两个相等的角,请直接写出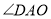 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】按照有关规定:距离铁轨道200米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物.
如图是一个小区平面示意图,矩形ABEF为一新建小区,直线MN为高铁轨道,C、D是直线MN上的两点,点C、A、B在一直线上,且DA⊥CA,∠ACD=30°.小王看中了①号楼A单元的一套住宅,与售楼人员的对话如下:

(1)小王心中一算,发现售楼人员的话不可信,请你通过计算用所学的数学知识说明理由.
(2)若一列长度为228米的高铁以70米/秒的速度通过时,则A单元用户受到影响时间有多长?( 温馨提示:
 ≈1.4,
≈1.4, ≈1.7,
≈1.7, ≈6.1)
≈6.1)
相关试题

