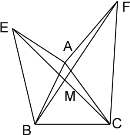
【题目】如图甲所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC. BF与CE相交于点M
(1)求证:①△ACE≌△AFB;②EC⊥BF.
(2)如图乙连接EF,画出△ABC边BC上的高线AD,延长DA交EF于点N,其他条件不变,下列四个结论:①∠EAN=∠ABC;
②△AEN≌△BAD;③![]() ;④EN=FN。
;④EN=FN。
正确的结论是____________(把正确结论的序号全部填上)

参考答案:
【答案】(1)见解析(2)①③④.
【解析】
(1)先根据AE⊥AB,AF⊥AC,AE=AB,AF=AC判定△ACE≌△AFB(SAS);再根据全等三角形的性质得出∠ACM=∠AFM,根据Rt△ACF中,∠AFM+∠MFC+∠ACF=90°,可得∠ACM+∠MFC+∠ACF=90°,即△MCF是直角三角形,进而得出结论;
(2)先作EH⊥AN,交AN于点H,FK⊥AN,交AN延长线于点K,构造三对全等三角形:△AEH≌△BAD,△AFK≌△ACD,△FKN≌△EHN,根据全等三角形的面积相等,即可得出S△ABD=S△EAH,S△FKA=S△ADC,S△ENH=S△FNK,根据S△ABC=S△ABD+S△ADC=S△AEH+S△AFK=(S△EAN-S△ENH)+(S△FNA+S△FNK)=S△EAN+S△FNA=S△AEF,即可得出结论③;最后根据△FKN≌△EHN,得出FN=EN即可.
(1)证明:①∵AE⊥AB,AF⊥AC,
∴∠BAE=∠CAF=90°,
∴∠BAF=∠EAC,
在△ACE和△AFB中,
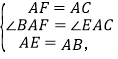
∴△ACE≌△AFB(SAS);
②∵△ACE≌△AFB,
∴∠ACM=∠AFM,
∵Rt△ACF中,∠AFM+∠MFC+∠ACF=90°,
∴∠ACM+∠MFC+∠ACF=90°,
即△MCF是直角三角形,
∴∠CMF=90°,即CE⊥BF;
(2)∵∠BAE=90°,AD⊥BD,
∴∠EAN+∠BAD=90°=∠ABC+∠BAD,
∴∠EAN=∠ABC,故①正确;
∵∠AEN与∠BAD不一定相等,
∴△AEN与△BAD不一定全等,故②错误;
作EH⊥AN,交AN于点H,FK⊥AN,交AN延长线于点K,
∴∠AEH+∠EAH=90°,
∵∠EAB=90°,
∴∠EAH+∠BAD=90°,
∴∠AEH=∠BAD,
在△AEH和△BAD中,

∴△AEH≌△BAD(AAS),
∴EH=AD,
同理可得:△AFK≌△ACD,
∴FK=AD,
∴FK=EH,
在△FKN和△EHN中,
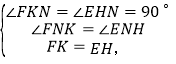
∴△FKN≌△EHN(AAS),
∴![]()
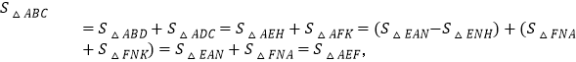 即
即![]() 故③正确;
故③正确;
∵△FKN≌△EHN,
∴FN=EN,故④正确.
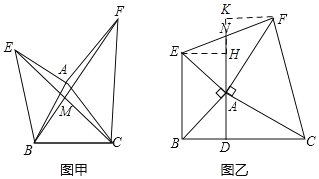
故答案为:①③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.

(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC= 度.
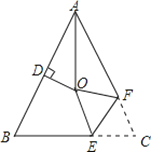
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60,且BQ=BP,连接CQ.
(1)观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2)若PA=3,PB=4,PC=5,连接PQ,试判断△PQC的形状,并说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若BC=EC,∠BCE=∠ACD,则添加不能使△ABC≌△DBC的条件是( )

A.AB=DE B.∠B=∠E C.AC=DC D.∠A=∠D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=6,BC=8,AB=10
(1)尺规作图:作AD平分∠CAB,交BC于点D;
(2)求CD的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+x﹣2与x轴交于A,B两点,与y轴交于点C.
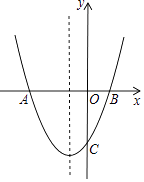
(1)求点A,点B和点C的坐标;
(2)在抛物线的对称轴上有一动点P,求PB+PC的值最小时的点P的坐标;
(3)若点M是直线AC下方抛物线上一动点,求四边形ABCM面积的最大值.
相关试题

