【题目】材料一:一个正整数x能写成x=a2﹣b2(a,b均为正整数,且a≠b),则称x为“雪松数”,a,b为x的一个平方差分解,在x的所有平方差分解中,若a2+b2最大,则称a,b为x的最佳平方差分解,此时F(x)=a2+b2.
例如:24=72﹣52,24为雪松数,7和5为24的一个平方差分解,32=92﹣72,32=62﹣22,因为92+72>62+22,所以9和7为32的最佳平方差分解,F(32)=92+72
材料二:若一个四位正整数,它的千位数字与个位数字相同,百位数字与十位数字相同,但四个数字不全相同,则称这个四位数为“南麓数”.例如4334,5665均为“南麓数”.
根据材料回答:
(1)请直接写出两个雪松数,并分别写出它们的一对平方差分解;
(2)试证明10不是雪松数;
(3)若一个数t既是“雪松数”又是“南麓数”,并且另一个“南麓数”的前两位数字组成的两位数与后两位数字组成的两位数恰好是t的一个平方差分解,请求出所有满足条件的数t中F(t)的最大值.
参考答案:
【答案】(1)112=112﹣32,40=72﹣32;(2)见解析;(3)12020.
【解析】试题分析:(1)根据雪松数的特征即可得到结论;
(2)根据题意即可得到结论;
(3)设t=![]() (a,b均为正整数,且0<a≠b≤9),另一个“南麓数”为t′=
(a,b均为正整数,且0<a≠b≤9),另一个“南麓数”为t′=![]() (m,n均为正整数,且0<n<m≤9),根据“南麓数”的特征即可得到结论.
(m,n均为正整数,且0<n<m≤9),根据“南麓数”的特征即可得到结论.
试题解析:解:(1)112=112﹣32,40=72﹣32;
(2)若10是“雪松数”,则可设a2﹣b2=10(a,b均为正整数,且a≠b),则(a+b)(a﹣b)=10.又∵10=2×5=10×1.∵a,b均为正整数,∴a+b>a﹣b,∴![]() ,或
,或![]() ,解得:
,解得:![]() 或
或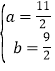 ,与a,b均为正整数矛盾,故10不是雪松数;
,与a,b均为正整数矛盾,故10不是雪松数;
(3)设t=![]() (a,b均为正整数,且0<a≠b≤9),另一个“南麓数”为t′=
(a,b均为正整数,且0<a≠b≤9),另一个“南麓数”为t′=![]() (m,n均为正整数,且0<n<m≤9),则t=(10m+n)2﹣(10n+m)2=99(m2﹣n2)=99(m+n)(m﹣n),∴99(m+n)(m﹣n)=1000a+100b+10b+a=1001a+110b,整理得,(m+n)(m﹣n)=10a+b+
(m,n均为正整数,且0<n<m≤9),则t=(10m+n)2﹣(10n+m)2=99(m2﹣n2)=99(m+n)(m﹣n),∴99(m+n)(m﹣n)=1000a+100b+10b+a=1001a+110b,整理得,(m+n)(m﹣n)=10a+b+![]() .∵a,b,m,n均为正整数,∴a+b=9,经探究
.∵a,b,m,n均为正整数,∴a+b=9,经探究![]() ,符合题意,∴t的值分别为:2772,5445,t′的值分别为:8668,8338,由材料一可知,F(t)的最大值为:862+682=12020.
,符合题意,∴t的值分别为:2772,5445,t′的值分别为:8668,8338,由材料一可知,F(t)的最大值为:862+682=12020.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,有一座拱桥圆弧形,它的跨度AB为60米,拱高PM为18米,当洪水泛滥到跨度只有30米时,就要采取紧急措施,若拱顶离水面只有4米,即PN=4米时,是否采取紧急措施?(
 =1.414)
=1.414) 
-
科目: 来源: 题型:
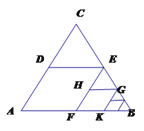
查看答案和解析>>【题目】如图,△ABC是面积为1的等边三角形。取BC边中点E,作ED∥AB,
EF∥AC,得到四边形EDAF,它的面积记做S1;取BE中点G,做GH∥FB,GK∥EF,
得到四边形GHFK,它的面积记作S2.照此规律作下去,
则S2018=__________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+4x+3交x轴于A、B两点,(A在B左侧),交y轴于点C.

(1)求A、B、C三点的坐标.
(2)求抛物线的对称轴及顶点坐标.
(3)抛物线上是否存在点F,使△ABF的面积为1?若存在,求F点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.

(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)x2﹣2x﹣8=0;
(2)3x(x﹣1)=2(x﹣1);
(3)x2+3=3(x+1);
(4)2x(4x+5)=7;
(5)4x2﹣8x+1=0;
(6)(y+2)2=(3y﹣1)2 . -
科目: 来源: 题型:
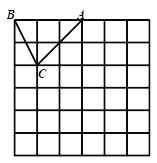
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
(1)在网格中画出△A1B1C1和△A1B2C2;
(2)计算线段AC从开始变换到A1 C2的过程中扫过区域的面积(重叠部分不重复计算)
相关试题

