搜索
【题目】如图，AD⊥BC于D，EG⊥BC于G，∠E=∠1，试说明AD平分∠BAC的理由．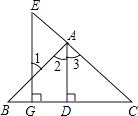 
参考答案：
【答案】解：∵AD⊥BC于D，EG⊥BC于G （已知） ∴∠ADC=∠EGC=90° （垂直定义）
∴AD∥EG （同位角相等，两直线平行）
∴∠1=∠2 （两直线平行，内错角相等）
∠3=∠E （两直线平行，同位角相等）
又∵∠E=∠1 （已知）
∴∠2=∠3 （等量代换）
∴AD平分∠BAC （角平分线定义）
【解析】先利用平面内垂直于同一条直线的两条直线互相平行，得到AD∥EG，再利用平行线的性质和已知条件求出∠2=∠3即可．
【考点精析】本题主要考查了平行线的判定与性质的相关知识点，需要掌握由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质才能正确解答此题．
-
科目： 来源： 题型：
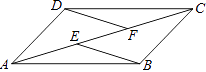
查看答案和解析>>【题目】已知，E、F是四边形ABCD的对角线AC上的两点，AE=CF，BE=DF，BE∥DF．求证：四边形ABCD是平行四边形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A，B在反比例函数
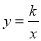（k＞0）的图象上，AC⊥x轴，BD⊥x轴，垂足C，D分别在x轴的正、负半轴上，CD=k，已知AB=2AC，E是AB的中点，且△BCE的面积是△ADE的面积的2倍，则k的值是______．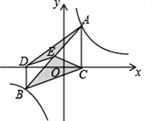
-
科目： 来源： 题型：
查看答案和解析>>【题目】学校早上8时上第一节课，45分钟后下课，这节课中分针转动的角度为（ ）
A.45°
B.90°
C.180°
D.270° -
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的方程x2+2x+m=0的有两个相等的实数根，则m为（ ）
A.2
B.﹣2
C.1
D.﹣1 -
科目： 来源： 题型：
查看答案和解析>>【题目】细观察，找规律 下列各图中的MA1与NAn平行．
（1）图①中的∠A1+∠A2=度， 图②中的∠A1+∠A2+∠A3=度，
图③中的∠A1+∠A2+∠A3+∠A4=度，
图④中的∠A1+∠A2+∠A3+∠A4+∠A5=度，
…，
第⑩个图中的∠A1+∠A2+∠A3+…+∠A11=度
（2）第n个图中的∠A1+∠A2+∠A3+…+∠An+1=
（3）请你证明图②的结论． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，∠1=∠2．求证：∠3+∠4=180° 证明：∵∠1=∠2（已知）
∴a∥b（）
∴∠3+∠5=180°（两直线平行，同旁内角互补）
又∵∠4=∠5（）
∴∠3+∠4=180°（等量代换）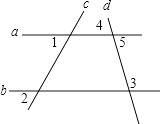
相关试题
