【题目】如图,直线y=mx+n与双曲线y= ![]() 相交于A(﹣1,2)、B(2,b)两点,与y轴相交于点C.
相交于A(﹣1,2)、B(2,b)两点,与y轴相交于点C.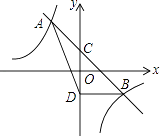
(1)求m,n的值;
(2)若点D与点C关于x轴对称,求△ABD的面积;
(3)在坐标轴上是否存在异于D点的点P,使得S△PAB=S△DAB?若存在,直接写出P点坐标;若不存在,说明理由.
参考答案:
【答案】
(1)解:∵点A(﹣1,2)在双曲线y= ![]() 上,
上,
∴2= ![]() ,
,
解得,k=﹣2,
∴反比例函数解析式为:y=﹣ ![]() ,
,
∴b= ![]() =﹣1,
=﹣1,
则点B的坐标为(2,﹣1),
∴ ![]() ,
,
解得,m=﹣1,n=1
(2)解:对于y=﹣x+1,当x=0时,y=1,
∴点C的坐标为(0,1),
∵点D与点C关于x轴对称,
∴点D的坐标为(0,﹣1),
∴△ABD的面积= ![]() ×2×3=3
×2×3=3
(3)解:对于y=﹣x+1,当y=0时,x=1,
∴直线y=﹣x+1与x轴的交点坐标为(0,1),
当点P在x轴上时,设点P的坐标为(a,0),
S△PAB= ![]() ×|1﹣a|×2+
×|1﹣a|×2+ ![]() ×|1﹣a|×1=3,
×|1﹣a|×1=3,
解得,a=﹣1或3,
当点P在y轴上时,设点P的坐标为(0,b),
S△PAB= ![]() ×|1﹣b|×2+
×|1﹣b|×2+ ![]() ×|1﹣b|×1=3,
×|1﹣b|×1=3,
解得,b=﹣1或3,
∴P点坐标为(﹣1,0)或(3,0)或(0,﹣1)或(0,3)
【解析】(1)由点A(﹣1,2)在双曲线上,得到k=﹣2,得到反比例函数解析式为,从而求出b的值和点B的坐标,把A、B坐标代入直线y=mx+n,求出m、n的值;(2)由一次函数的解析式求出点C的坐标,由点D与点C关于x轴对称,得到点D的坐标,从而求出△ABD的面积;(3)由一次函数的解析式得到直线y=﹣x+1与x轴的交点坐标为(0,1),当点P在x轴上时,设点P的坐标为(a,0),求出S△PAB=3,求出a的值,当点P在y轴上时,设点P的坐标为(0,b),求出S△PAB=3,求出b的值,从而得到P点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:图1、图2是两张形状、大小完全相同的网格,网格中的每个小正方形的边长均为
 .格中各有一个完全相同的三角形,请在图1、图2分别面一条直线,满足以下要求
.格中各有一个完全相同的三角形,请在图1、图2分别面一条直线,满足以下要求
(1)直线与三角形的交点要经过网格的格点(每个小正方形的顶点均为格点)
(2)在图1、图2中分别用不同的方法将三角形分成两个图形其中一个是三角形另一个是四边形,分割后的三角形的面积记为
 ,四边形的面积为
,四边形的面积为 ,且
,且 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是腰长为1的等腰直角三形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2018个等腰直角三角形的斜边长是______.
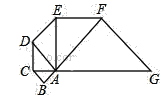
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=9,AD=6,∠ADC的平分线交AB于点E,交CB的延长线于点F,AG⊥DE,垂足为G.若AG=4
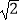 ,则△BEF的面积是( )
,则△BEF的面积是( )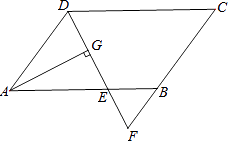
A.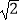
B.2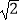
C.3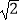
D.4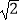
-
科目: 来源: 题型:
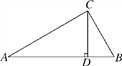
查看答案和解析>>【题目】如图,在Rt△ABC中,CD⊥AB,垂足为D,如果CD=12,AD=16,BD=9,那么△ABC是直角三角形吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋中有3张形状大小完全相同的卡片,编号为1,2,3,先任取一张,将其编号记为m,再从剩下的两张中任取一张,将其编号记为n.
(1)请用树状图或者列表法,表示事件发生的所有可能情况;
(2)求关于x的方程x2+mx+n=0有两个不相等实数根的概率.
相关试题

