【题目】如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
解:∵AD∥BC,( )
∴∠ACB+∠DAC=180° ,( )
∵∠DAC=120°,(已知)
∴∠ACB=180°﹣∠DAC= °.
∵∠ACF=20°(已知),
∴∠BCF=∠ACB﹣∠ACF= °.
∵CE平分∠BCF,
∴∠BCE=![]() ∠BCF= °.
∠BCF= °.
∵EF∥AD,AD∥BC,
∴EF∥ ,( )
∴∠FEC=∠BCE= °.( )

参考答案:
【答案】已知;两直线平行,同旁内角互补;60;40;20;BC,平行于同一直线的两直线平行;20,两直线平行,内错角相等.
【解析】根据平行线的性质求出∠ACB,求出∠BCF,根据角平分线性质求出∠BCE,根据平行线的性质求出即可.
∵AD∥BC(已知)
∴∠ACB+∠DAC=180° ( 两直线平行,同旁内角互补 )
∵∠DAC=120°(已知)
∴∠ACB=180°﹣∠DAC= 60 °
∵∠ACF=20°(已知)
∴∠BCF=∠ACB﹣∠ACF= 40 °
∵CE平分∠BCF
∴∠BCE=![]() ∠BCF= 20 °
∠BCF= 20 °
∵EF∥AD,AD∥BC
∴EF∥ BC ( 平行于同一直线的两直线平行 )
∴∠FEC=∠BCE= 20 °( 两直线平行,内错角相等 )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点P(6,3),过点P作PM⊥x轴于点M,PN⊥y轴于点N,反比例函数y=
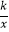 的图象交PM于点A,交PN于点B.若四边形OAPB的面积为12,则k= .
的图象交PM于点A,交PN于点B.若四边形OAPB的面积为12,则k= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一面积为5
 的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为 .
的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为2的菱形ABCD中,∠A=60°,点M是AD边的中点,连接MC,将菱形ABCD翻折,使点A落在线段CM上的点E处,折痕交AB于点N,则线段EC的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形AOCB的两边OA、OC分别在x轴和y轴上,且OA=2,OC=1.在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的
 倍,得到矩形A1OC1B1 , 再将矩形A1OC1B1以原点O为位似中心放大
倍,得到矩形A1OC1B1 , 再将矩形A1OC1B1以原点O为位似中心放大  倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 .
倍,得到矩形A2OC2B2…,以此类推,得到的矩形AnOCnBn的对角线交点的坐标为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣4,0),C(0,0)

(1)画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
(2)画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O;
(3)在x轴上存在一点P,满足点P到A1与点A2距离之和最小,请直接写出P点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某物流公司引进A,B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,根据图象提供的信息,解答下列问题:

(1)求yB关于x的函数解析式;
(2)如果A,B两种机器人连续搬运5小时,那么B种机器人比A种机器人多搬运了多少千克?
相关试题

