【题目】如图, ![]() 中,∠
中,∠![]() =90°,
=90°,![]() 是斜边
是斜边![]() 上的中线,分别过点
上的中线,分别过点![]() 作
作![]() ∥
∥![]() ,
, ![]() ∥
∥![]() ,两线交于点
,两线交于点![]() .
.
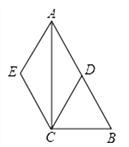
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,
, ![]() ,求四边形
,求四边形![]() 的面积.
的面积.
参考答案:
【答案】(1)证明见解析;
(2)![]() 菱形AECD
菱形AECD![]()
【解析】试题分析:(1)直接利用平行四边形的判定方法得出四边形AECD是平行四边形,再利用直角三角形的性质得出CD=AD,即可得出四边形AECD是菱形;(2)利用菱形的性质和平行四边形的性质得出AC,ED的长,进而得出菱形面积.
试题解析:(1)证明:∵AE∥DC,CE∥AB,
∴四边形AECD是平行四边形,
∵Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,
∴CD=AD,
∴四边形AECD是菱形;
(2)连接DE.
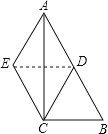
∵∠ACB=90°,∠B=60°,
∴∠BAC=30°
∴AB=4,AC=![]() ,
,
∵四边形AECD是菱形,
∴EC=AD=DB,
又∵EC∥DB
∴四边形ECBD是平行四边形,
∴ED=CB=2,
∴S菱形AECD=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
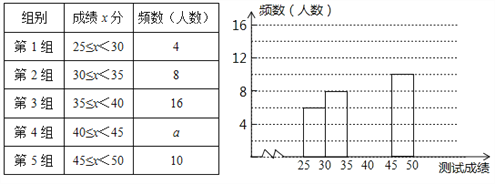
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
-
科目: 来源: 题型:
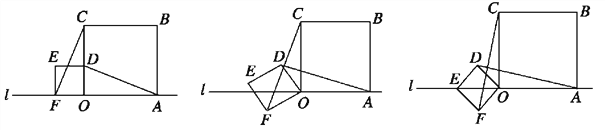
查看答案和解析>>【题目】小明在数学活动课上,将边长为
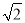 和3的两个正方形放置在直线l上,如图a,他连接AD、CF,经测量发现AD=CF.
和3的两个正方形放置在直线l上,如图a,他连接AD、CF,经测量发现AD=CF.(1)他将正方形ODEF绕O点逆时针针旋转一定的角度,如图b,试判断AD与CF还相等吗?说明理由.
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图c,请求出CF的长.
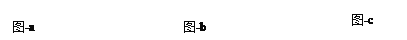
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,有若干张边长为
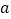 的小正方形①、长为
的小正方形①、长为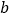 宽为
宽为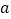 的长方形②以及边长为
的长方形②以及边长为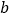 的大正方形③的纸片.
的大正方形③的纸片.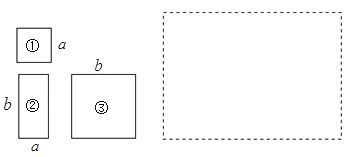
(1)已知小正方形①与大正方形③的面积之和为169,长方形②的周长为34,求长方形②的面积.
(2)如果现有小正方形①1张,大正方形③2张,长方形②3张,请你将它们拼成一个大长方形 (在图2虚线框内画出图形),并运用面积之间的关系,将多项式
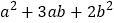 分解因式.
分解因式. -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市用3000元购进某种干果销售,由于销售状况良好,超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量是第一次的2倍还多300千克,如果超市按每千克9元的价格出售,当大部分干果售出后,余下的600千克按售价的8折售完.
(1)该种干果的第一次进价是每千克多少元?
(2)超市销售这种干果共盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°

(1)先作∠ACB的平分线交AB边于点P,再以点P为圆心,PA长为半径作⊙P;(要求:尺规作图,保留作图痕迹,不写作法)
(2)请你判断(1)中BC与⊙P的位置关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据2,3,1,3,5,4,这组数据的众数是___________.
相关试题

