【题目】已知如图所示, ![]() 与
与 ![]() 关于点
关于点 ![]() 成中心对称,连接
成中心对称,连接 ![]() ,
, ![]() .
.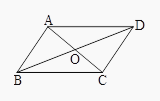
(1)求证:四边形 ![]() 是平行四边形;
是平行四边形;
(2)若 ![]() 的面积为15
的面积为15 ![]() ,求四边形
,求四边形 ![]() 的面积.
的面积.
参考答案:
【答案】
(1)
证明:∵ ![]() 与
与 ![]() 关于点
关于点 ![]() 成中心对称,∴
成中心对称,∴ ![]() 即四边形
即四边形 ![]() 的对角线互相平分,∴四边形
的对角线互相平分,∴四边形 ![]() 是平行四边形.
是平行四边形.
(2)
解:记 ![]() 底边上的高为h,那么平行四边形ABCD底边AB上的为2h,因为
底边上的高为h,那么平行四边形ABCD底边AB上的为2h,因为 ![]() 的面积为15,所以
的面积为15,所以 ![]() ,所以2ABh=60,所以平行四边形ABCD的面积为60
,所以2ABh=60,所以平行四边形ABCD的面积为60 ![]() .
.
【解析】(2)的关键在于明白: ![]() 底边上的高为平行四边形ABCD底边AB上的为一半.
底边上的高为平行四边形ABCD底边AB上的为一半.
【考点精析】根据题目的已知条件,利用平行四边形的判定和中心对称及中心对称图形的相关知识可以得到问题的答案,需要掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;如果把一个图形绕着某一点旋转180度后能与另一个图形重合,那么我们就说,这两个图形成中心对称;如果把一个图形绕着某一点旋转180度后能与自身重合,那么我们就说,这个图形成中心对称图形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016·天津)公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆,已知每辆甲种货车一次最多运送机器45台,租车费用为400元,每辆乙种货车一次最多运送机器30台,租车费用为280元.
(1)设租用甲种货车x辆(x为非负整数),试填写表格:
表一:
租用甲种货车的数量 / 辆
3
7
x
租用的甲种货车最多运送机器的数量 / 台
135
租用的乙种货车最多运送机器的数量 / 台
150
表二:
租用甲种货车的数量 / 辆
3
7
x
租用甲种货车的费用/ 元
2800
租用乙种货车的费用 / 元
280
(2)若租用甲种货车x辆时,设两种货车的总费用为y元,试确定能完成此项运送任务的最节省费用的租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 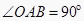 ,
, 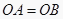 ,将
,将  绕点O沿逆时针方向旋转
绕点O沿逆时针方向旋转  得到
得到  ,连结
,连结 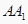 ,求证:四边形
,求证:四边形  是平行四边形.
是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列做法正确的是( )
A. 由2(x+1)=x+7去括号、移项、合并同类项,得x=5
B. 由
 =1+
=1+ 去分母,得2(2x﹣1)=1+3(x﹣3)
去分母,得2(2x﹣1)=1+3(x﹣3)C. 由2(2x﹣1)﹣3(x﹣3)=1去括号,得4x﹣2﹣3x﹣9=1
D. 由7x=4x﹣3移项,得7x﹣4x=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个有进水管与出水管的容器,从某时刻开始4 min内只进水不出水,在随后的8 min内既进水又出水,每分的进水量和出水量是两个常数.容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.

(1)当4≤x≤12时,求y关于x的函数解析式;
(2)直接写出每分进水,出水各多少升.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我国古代数学著作《九章算术》中记载了一道有趣的数学问题:“今有凫(凫:野鸭)起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”意思是:野鸭从南海起飞,7天飞到北海;大雁从北海起飞,9天飞到南海.野鸭与大雁从南海和北海同时起飞,经过几天相遇.设野鸭与大雁从南海和北海同时起飞,经过x天相遇,根据题意,下面所列方程正确的是( )
A. (9-7)x=1 B. (9-7)x=1 C. (
 +
+ )x=1 D. (
)x=1 D. ( -
- )x=1
)x=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中既是中心对称图形又是轴对称图形的是( )
A.
B.
C.
D.
相关试题

