【题目】如图,在△ABC中,点D是∠ACB与∠ABC的角平分线的交点,BD的延长线交AC于点E.

(1)若∠A=80°,求∠BDC的度数;
(2)若∠EDC=40°,求∠A的度数;
(3)请直接写出∠A与∠BDC之间的数量关系(不必说明理由).
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)∠BDC=
(3)∠BDC=![]()
【解析】
(1)首先根据∠A=80°,便可计算出![]() 的度数,再根据BD、CD平分
的度数,再根据BD、CD平分![]() 和
和![]() ,再结合
,再结合![]() 便可计算的∠BDC的度数;
便可计算的∠BDC的度数;
(2)根据∠EDC=40°,可计算的![]() 的度数,再结合
的度数,再结合![]() 可得
可得![]() ,再根据BD、CD平分
,再根据BD、CD平分![]() 和
和![]() ,在△ABC中便可计算出∠A的度数;
,在△ABC中便可计算出∠A的度数;
(3)根据(1)和(2)中的计算可直接写出∠A与∠BDC之间的数量关系
(1)在△ABC中
![]() ∠A=80°
∠A=80°
![]()
![]()
![]() BD、CD平分
BD、CD平分![]() 和
和![]()
![]()
![]()
在![]() 中,∠BDC=
中,∠BDC=![]()
(2)在![]() 中
中
![]() ∠EDC=40°
∠EDC=40°
![]()
![]()
![]()
![]()
![]() BD、CD平分
BD、CD平分![]() 和
和![]()
![]()
![]()
在△ABC中![]()
(3)根据(1)和(2)可得∠BDC=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在一块宽为12m,长为20m的矩形地面上修筑同样宽的道路,余下的部分种上草坪.要使草坪的面积为180m2,求道路的宽;
(2)现在对该矩形区域进行改造,如图2,在正中央建一个与矩形的边互相平行的正方形观赏亭,观赏亭的四边连接四条与矩形的边互相平行的且宽度相等的道路,已知道路的宽为正方形边长的
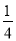 .若道路与观赏亭的面积之和是矩形面积的
.若道路与观赏亭的面积之和是矩形面积的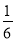 ,求道路的宽.
,求道路的宽.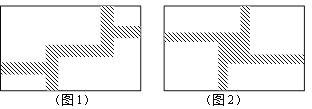
【答案】(1)道路宽为2米;(2)道路的宽为1米.
【解析】试题分析:(1)设道路宽为x米,利用平移把不规则的图形变为规则图形,如此一来,所有草坪面积之和就变为了(20﹣x)(12﹣x)米2,进而即可列出方程,求出答案;
(2)设道路的宽为x米,则正方形边长为4x,根据道路与观赏亭的面积之和是矩形面积的
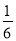 ,列方程求解即可.
,列方程求解即可.试题解析:解:(1)设道路宽为x米,
根据题意得:(20﹣x)(12﹣x)=180
解得:x1=30(舍去),x2=2
答:道路宽为2米;
(2)设道路的宽为x米,
则可列方程:x(12-4x)+x(20-4x)+16x2=
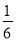 ×20×12,
×20×12,即:x2+4x-5=0,
解得:x1=1,x2=-5(舍去),
答:道路的宽为1米.
点睛:考查了一元二次方程的应用,这类题目体现了数形结合的思想,需利用平移把不规则的图形变为规则图形,进而即可列出方程,求出答案.另外还要注意解的合理性,从而确定取舍.
【题型】解答题
【结束】
10【题目】如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.在图3中,将三棱柱沿过点A的侧棱剪开,得到如图4的侧面展开图.为了得到裁剪的角度,我们可以根据展开图拼接出符合条件的平行四边形进行研究.
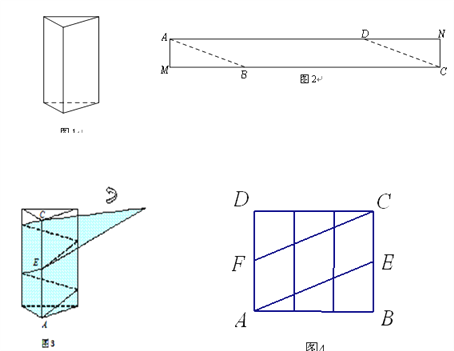
(1)请在图4中画出拼接后符合条件的平行四边形;
(2)请在图2中,计算裁剪的角度(即∠ABM的度数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

-
科目: 来源: 题型:
查看答案和解析>>【题目】为实现营养的合理搭配,某电商推出适合不同人群的甲、乙两种袋装混合粗粮.其中,甲种袋装粗粮每袋装有3千克A粗粮,1千克B粗粮,1千克C粗粮;乙种袋装粗粮每袋装有1千克A粗粮,2千克B粗粮,2千克C粗粮.甲、乙两种袋装粗粮每袋成本价分别为袋中的A、B、C三种粗粮的成本价之和.已知A粗粮每千克成本价为6元,甲种粗粮每袋售价为71.5元,利润率为30%,乙种粗粮利润率为20%,则乙种粗粮每袋的售价为________元.(利润率=
 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=45°,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.
(1)求证:
 ;
;(2)设EF=x,当x为何值时,矩形EFPQ的面积最大?并求其最大值;
(3)当矩形EFPQ的面积最大时,该矩形EFPQ以每秒1个单位的速度沿射线QC匀速运动(当点Q与点C重合时停止运动),设运动时间为t秒,矩形EFFQ与△ABC重叠部分的面积为S,求S与t的函数关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产A、B两种产品共50件,需购买甲、乙两种材料.生产一件A产品需甲种材料30千克、乙种材料10千克;生产一件B产品需甲、乙两种材料各20千克.经测算,购买甲、乙两种材料各1千克共需资金40元,购买甲种材料2千克和乙种材料3千克共需资金105元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过38000元,且生产B产品不少于28件,问符合条件的生产方案有哪几种?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.

(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
相关试题

