搜索
【题目】已知P（x，y）为不等式组 
表示的平面区域M内任意一点，若目标函数z=5x+3y的最大值等于平面区域M的面积，则m= ．
参考答案：
【答案】-2
【解析】解：作出不等式组对应的平面区域如图：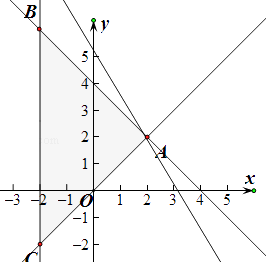 
由z=5x+3y得y=﹣ 
x+ 
，
平移直线y=﹣ x+ ，
由图象知当直线y=﹣ x+ ，经过点A时，直线的截距最大，此时z最大，
由 
，解得x=y=2，即A（2，2），
此时z=5×2+3×2=16，
由 
．解得x=a，y=4﹣a，即B（a，4﹣a），
由 
，解得x=y=a，即C（a，a），
∴BC=4﹣a﹣a=4﹣2a，△ABC的高为2﹣a，
∴S△ABC= 
×（2﹣a）（4﹣2a）=（2﹣a）2=16，
解得a=﹣2，a=6（舍去），
所以答案是：﹣2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】《张邱建算经》是中国古代数学史上的杰作，该书中有首古民谣记载了一数列问题：“南山一棵竹，竹尾风割断，剩下三十节，一节一个圈．头节高五寸① ， 头圈一尺三② ． 逐节多三分③ ， 逐圈少分三④ ． 一蚁往上爬，遇圈则绕圈．爬到竹子顶，行程是多远？”（注释：①第一节的高度为0.5尺；②第一圈的周长为1.3尺；③每节比其下面的一节多0.03尺；④每圈周长比其下面的一圈少0.013尺） 问：此民谣提出的问题的答案是（ ）
A.72.705尺
B.61.395尺
C.61.905尺
D.73.995尺 -
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图1是由大小相同的小立方块搭成的几何体，请在图2的方格中画出从上面和左面看到的该几何体的形状图．（只需用2B铅笔将虚线化为实线）
（2）若要用大小相同的小立方块搭一个几何体，使得它从上面和左面看到的形状图与你在图2方格中所画的形状图相同，则搭这样的一个几何体最多需要 个小立方块．
-
科目： 来源： 题型：
查看答案和解析>>【题目】设函数f（x）=|x2﹣2x﹣1|，若m＞n＞1，且f（m）=f（n），则mn的取值范围为（ ）
A.
B.
C.（1，3）
D.（1，3] -
科目： 来源： 题型：
查看答案和解析>>【题目】已知数列{an}中，a1＜0，an+1=
，数列{bn}满足：bn=nan（n∈N*），设Sn为数列{bn}的前n项和，当n=7时Sn有最小值，则a1的取值范围是 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，角A，B，C的对边分别为a，b，c，且
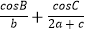=0． （Ⅰ）求角B的大小；
（Ⅱ）若b=
，a+c=4，求△ABC的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】某网络营销部门为了统计某市网友2016年12月12日的网购情况，从该市当天参与网购的顾客中随机抽查了男女各30人，统计其网购金额，得到如下频率分布直方图：
网购达人
非网购达人
合计
男性
30
女性
12
30
合计
60
若网购金额超过2千元的顾客称为“网购达人”，网购金额不超过2千元的顾客称为“非网购达人”．
（Ⅰ）若抽取的“网购达人”中女性占12人，请根据条件完成上面的2×2列联表，并判断是否有99%的把握认为“网购达人”与性别有关？
（Ⅱ）该营销部门为了进一步了解这60名网友的购物体验，从“非网购达人”、“网购达人”中用分层抽样的方法确定12人，若需从这12人中随机选取3人进行问卷调查．设ξ为选取的3人中“网购达人”的人数，求ξ的分布列和数学期望．
（参考公式：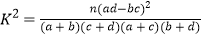
，其中n=a+b+c+d）P（K2≥k）
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
相关试题
