【题目】已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C、D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.

参考答案:
【答案】(1)证明见解析;(2)8-2![]() .
.
【解析】试题分析:(1)过O作OE⊥AB,根据垂径定理得到AE=BE,CE=DE,从而得到AC=BD;
(2)由(1)可知,OE⊥AB且OE⊥CD,连接OC,OA,再根据勾股定理求出CE及AE的长,根据AC=AE﹣CE即可得出结论.
试题解析:(1)作OE⊥AB,
∵AE=BE,CE=DE,
∴BE﹣DE=AE﹣CE,即AC=BD;
(2)∵由(1)可知,OE⊥AB且OE⊥CD,连接OC,OA,∴OE=6,
∴CE=![]() ,
,
AE=![]() ,
,
∴AC=AE﹣CE=8﹣2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在⊙O中,AC、BC是弦,根据条件填空:
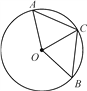
(1)若AC=BC,则________________;
(2)若
 ,则______________;
,则______________;(3)若∠AOC=∠BOC,则______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列的说法中,正确的是 ( )
A. 会重合的图形一定是轴对称图形.
B. 中心对称图形一定是会重合的图形.
C. 两个成中心对称的图形的对称点连线必过对称中心.
D. 两个会重合的三角形一定关于某一点成中心对称.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A.a2+a3=a5
B.a3a4=a12
C.a6÷a3=a2
D.4a﹣a=3a -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某地有一座圆弧形拱桥,桥下水面宽度AB为7.2 m,拱高CD为2.4 m.
(1)求拱桥的半径;
(2)现有一艘宽3 m,船舱顶部为长方形并高出水面2 m的货船要经过这里,问此货船能顺利通过拱桥吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】用尺规作一个直角三角形,使其两条直角边分别等于已知线段时,实际上就是已知的条件是( )
A.三角形的两条边和它们的夹角
B.三角形的三边
C.三角形的两个角和它们的夹边
D.三角形的三个角 -
科目: 来源: 题型:
查看答案和解析>>【题目】CD是⊙O的一条弦,作直径AB,使AB⊥CD,垂足为E,若AB=10,CD=8,则BE的长是( )
A.8
B.2
C.2或8
D.3或7
相关试题

