【题目】在△ABC中,AB=AC=5,cos∠ABC=0.6,将△ABC绕点C顺时针旋转,得到△A1B1C.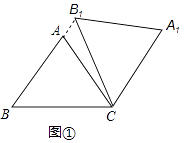
(1)如图1,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;
(2)如图2,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.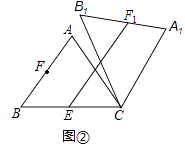
参考答案:
【答案】
(1)①证明:∵AB=AC,B1C=BC,
∴∠BB1C=∠B,∠B=∠ACB,
∵∠A1CB1=∠ACB(旋转角相等),
∴∠BB1C=∠A1CB1,
∴BB1∥CA1,
②过A作AF⊥BC于F,过C作CE⊥AB于E,

∵AB=AC,AF⊥BC,
∴BF=CF,
∵cos∠ABC=0.6,AB=5,
∴BF=3,
∴BC=6∴B1C=BC=6
∵CE⊥AB,
∴BE=B1E= ![]() ×6=
×6= ![]() ,
,
∴BB1= ![]() ,CE=
,CE= ![]() ,
,
∴AB1= ![]() ,
,
∴△AB1C的面积为: ![]() =
= ![]()
(2)解:如图3,
过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,EF1有最小值.
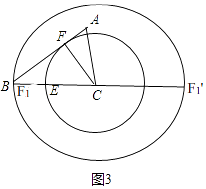
此时在Rt△BFC中,CF=4.8,
∴CF1=4.8,
∴EF1的最小值为4.8﹣3=1.8;
如图,以C为圆心BC为半径画圆交BC的延长线于F1',EF1'有最大值.
此时EF1'的最大值为EC+CF1'=3+6=9,
∴线段EF1的最大值与最小值的差为9﹣1.8=7.2.
【解析】(1)①根据旋转的性质和平行线的性质可证得BB1∥CA1;②过A作AF⊥BC于F,过C作CE⊥AB于E,根据等腰三角形的性质、解直角三角形及三角形的面积公式,即可求得答案。
(2)此题转化到圆中求解,过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,可求得EF1的最小值,以C为圆心BC为半径画圆交BC的延长线于F1',求得EF1'的最大值,即可求得线段EF1的最大值与最小值的差。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.
采购数量(件)
1
2
…
A产品单价(元/件)
1480
1460
…
B产品单价(元/件)
1290
1280
…
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的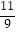 ,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润. -
科目: 来源: 题型:
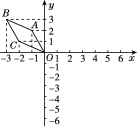
查看答案和解析>>【题目】如图,在平面直角坐标系中,O,A,B,C的坐标分别为(0,0),(-1,2),(-3,3)和(-2,1).
(1)若图中的各个点的纵坐标不变,横坐标都乘-1,与原图案相比,所得图案有什么变化?画出图形并说明一下变化.
(2)若图中的各个点的横坐标不变,纵坐标都乘-1,与原图案相比,所得图案有什么变化?画出图形并说明一下变化.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1 , 得∠A1;∠A1BC和∠A1CD的平分线交于点A2 , 得∠A2;…∠A2016BC和∠A20l6CD的平分线交于点A2017 , 则∠A2017=°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )
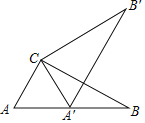
A. 12 B. 6 C. 6
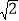 D.
D. 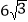
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣
 ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的解析式及A、B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ的最小值( )
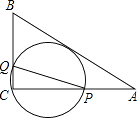
A.5
B.4
C.4.75
D.4.8
相关试题

