【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣ ![]() ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的解析式及A、B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
参考答案:
【答案】
(1)解:由题意,设抛物线的解析式为y=a(x﹣4)2﹣ ![]() (a≠0)
(a≠0)
∵抛物线经过(0,2)
∴a(0﹣4)2﹣ ![]() =2
=2
解得:a= ![]()
∴y= ![]() (x﹣4)2﹣
(x﹣4)2﹣ ![]()
即:y= ![]() x2﹣
x2﹣ ![]() x+2
x+2
当y=0时, ![]() x2﹣
x2﹣ ![]() x+2=0
x+2=0
解得:x=2或x=6
∴A(2,0),B(6,0)
(2)解:存在,如图2,
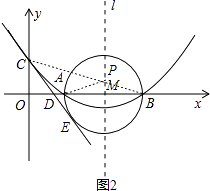
由(1)知:抛物线的对称轴l为x=4,
因为A、B两点关于l对称,连接CB交l于点P,则AP=BP,所以AP+CP=BC的值最小
∵B(6,0),C(0,2)
∴OB=6,OC=2
∴BC=2 ![]() ,
,
∴AP+CP=BC=2 ![]()
∴AP+CP的最小值为2 ![]()
(3)解:如图3,连接ME
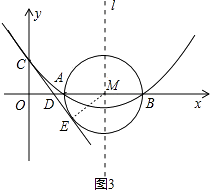
∵CE是⊙M的切线
∴ME⊥CE,∠CEM=90°
∵C的坐标(0,2),
∴OC=2,
∵AB=4,
∴ME=2
∴OC=ME=2,
∵∠ODC=∠MDE,
∵在△COD与△MED中
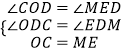
∴△COD≌△MED(AAS),
∴OD=DE,DC=DM
设OD=x
则CD=DM=OM﹣OD=4﹣x
则Rt△COD中,OD2+OC2=CD2,
∴x2+22=(4﹣x)2
∴x= ![]()
∴D( ![]() ,0)
,0)
设直线CE的解析式为y=kx+b(k≠0),
∵直线CE过C(0,2),D( ![]() ,0)两点,
,0)两点,
则 
解得: 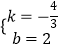
∴直线CE的解析式为y=﹣ ![]() +2;
+2;
【解析】(1)已知顶点坐标,因此函数解析式设成顶点式,再将点C的坐标代入即可求得函数解析式,由y=0,建立方程求解即可得到抛物线与x轴的两交点坐标。
(2)要在抛物线的对称轴l上求作点P,使AP+CP的值,抛物线是关于对称轴对称,点A关于直线l的对称点是点B,因此连接BC交直线l于点P,要求AP+CP的值,可证得AP+CP=BC,再Rt△OBC中根据勾股定理即可求出BC的长。
(3)由已知点A、B的坐标及AB时直径,可证得OC=ME,即可证明△COD≌△MED,得出OD=DE,DC=DM。运用勾股定理Rt△COD中,求出OD的长,即可求出点D的坐标,利用待定系数法,即可直线CE的解析式。
【考点精析】认真审题,首先需要了解确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法),还要掌握切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1 , 得∠A1;∠A1BC和∠A1CD的平分线交于点A2 , 得∠A2;…∠A2016BC和∠A20l6CD的平分线交于点A2017 , 则∠A2017=°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC=5,cos∠ABC=0.6,将△ABC绕点C顺时针旋转,得到△A1B1C.
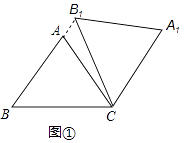
(1)如图1,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;
(2)如图2,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.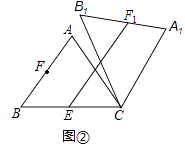
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )
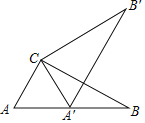
A. 12 B. 6 C. 6
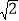 D.
D. 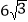
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ的最小值( )
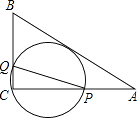
A.5
B.4
C.4.75
D.4.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:|
 ﹣2|+3tan30°+(
﹣2|+3tan30°+(  )﹣1﹣(3﹣π)0﹣
)﹣1﹣(3﹣π)0﹣  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD丄AC 于D,EF丄AC 于F.∠AMD=∠AGF.∠1=∠2=35°
(1)求∠GFC的度数:
(2)求证:DM∥BC.

相关试题

