【题目】下列方程没有实数解的是( )
A. ![]() =0 B.
=0 B. ![]() =x C.
=x C. ![]() =1 D.
=1 D. ![]() ﹣2x+3=0
﹣2x+3=0
参考答案:
【答案】D
【解析】
A、将方程左边分解因式,利用两数相乘积为0,两因式中至少有一个为0即可求出方程的解,作出判断;
B、将方程左右两边平方转化为一个一元二次方程,求出方程的解,经检验即可得到原方程的解,作出判断;
C、将方程左边的分子利用平方差公式分解因式,约分后得到一元一次方程,求出一次方程的解得到x的值,将x的值代入原方程进行检验,即可作出判断;
D、找出一元二次方程中的a,b及c,计算出b2-4ac,根据b2-4ac的正负即可判断出方程是否有解.
A、x4+x2=0,变形得:x2(x2+1)=0,
解得:x=0,本选项不合题意;
B、![]() =x,两边平方得:x+1=x2,即x2-x-1=0,
=x,两边平方得:x+1=x2,即x2-x-1=0,
解得:![]() ,
,
经检验![]() 不合题意,舍去,
不合题意,舍去,
∴![]() ,本选项不合题意;
,本选项不合题意;
C、![]() =x+2=1,
=x+2=1,
解得:x=-1,
经检验,x=-1是原方程的解,本选项不合题意;
D、x2-2x+3=0,
∵b2-4ac=(-2)2-4×3=-8<0,
∴此方程无解,本选项符合题意.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,E是BC的中点,连接AE、AC.
(1)点F是DC上一点,连接EF,交AC于点O(如图1),求证:△AOE∽△COF;
(2)若点F是DC的中点,连接BD,交AE与点G(如图2),求证:四边形EFDG是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017甘肃省天水市)△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=2,CQ=9时BC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我国边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防部迅速派出快艇B追赶(如图1).图2中l1、l2分别表示两船相対于海岸的距离s(海里)与追赶时间t(分)之间的关系.根据图象问答问题:
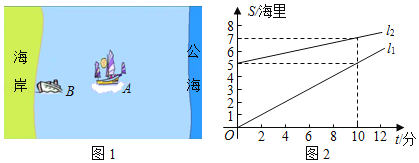
(1)①直线l1与直线l2中 表示B到海岸的距离与追赶时间之间的关系
②A与B比较, 速度快;
③如果一直追下去,那么B (填能或不能)追上A;
④可疑船只A速度是 海里/分,快艇B的速度是 海里/分
(2)l1与l2对应的两个一次函数表达式S1=k1t+b1与S2=k2t+b2中,k1、k2的实际意义各是什么?并直接写出两个具体表达式
(3)15分钟内B能否追上A?为什么?
(4)当A逃离海岸12海里的公海时,B将无法对其进行检查,照此速度,B能否在A逃入公海前将其拦截?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=6,BC=8,动点P从A点出发,以1cm/s的速度,沿A—C—B向B点运动,同时,动点Q从C点出发,以2cm/s的速度,沿C—B—A向A点运动,当其中一点运动到终点时,两点同时停止运动。设运动时间为t秒,当t=_______秒时,△PCQ的面积等于8cm2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
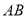 是
是 的直径,
的直径, 、
、 是弧
是弧 (异于
(异于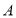 、
、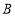 )上两点,
)上两点,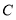 是弧
是弧 上一动点,
上一动点, 的角平分线交
的角平分线交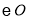 于点
于点 ,
,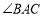 的平分线交
的平分线交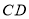 于点
于点 .当点
.当点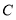 从点
从点 运动到点
运动到点 时,则
时,则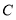 、
、 两点的运动路径长的比是( )
两点的运动路径长的比是( )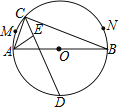
A.
 B.
B.  C.
C. 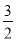 D.
D. 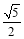
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1﹣x2)2+m2=21,求m的值.
相关试题

