Question

【题目】在平面直角坐标系中，已知△ABC三个顶点的坐标分别为A（﹣1，2），B（﹣3，4），C（﹣2，9）．
（1）画出△ABC，并求出AC所在直线的解析式．
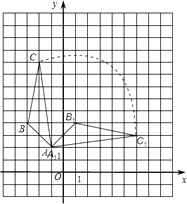
（2）画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1 ， 并求出△ABC在上述旋转过程中扫过的面积．

Answer 1

【答案】
（1）解：如图所示，△ABC即为所求，

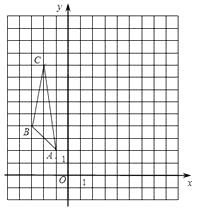
设AC所在直线的解析式为y=kx+b（k≠0），

∵A（﹣1，2），C（﹣2，9），

∴ ，

解得 ，

∴y=﹣7x﹣5

（2）解：如图所示，△A1B1C1即为所求，

由图可知， ，

S=S扇形+S△ABC，

= +2×7﹣1×5× ﹣1×7× ﹣2×2× ，

= ．

【解析】（1）利用待定系数法将A（﹣1，2），C（﹣2，9）代入解析式求出一次函数解析式即可；（2）根据AC的长度，求出S=S扇形+S△ABC ， 就即可得出答案．
【考点精析】本题主要考查了确定一次函数的表达式和扇形面积计算公式的相关知识点，需要掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）才能正确解答此题．