【题目】如图,P是正△ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB. 
(1)求旋转角的度数;
(2)求点P与点P′之间的距离;
(3)求∠APB的度数.
参考答案:
【答案】
(1)解:由∠BAC=60°可知旋转角的度数为60°
(2)解:连接PP′,由题意可知AP′=AP=6,
∵旋转角的度数为60°,
∴∠PAP′=60°.
∴△APP′为等边三角形,
∴PP′=AP=AP′=6

(3)解:∵BP′=PC=10,BP=8,PP′=6,
∴PP′2+BP2=BP′2,
∴△BPP′为直角三角形,且∠BPP′=90°
∴∠APB=∠BPP′+∠APP′=90°+60°=150°
【解析】(1)由∠BAC=60°可知旋转角的度数为60°;(2)由已知△PAC绕点A逆时针旋转后,得到△P′AB,可得△PAC≌△P′AB,PA=P′A,旋转角∠P′AP=∠BAC=60°,所以△APP′为等边三角形,即可求得PP′;(3)由△APP′为等边三角形,得∠APP′=60°,在△PP′B中,已知三边,用勾股定理逆定理证出直角三角形,得出∠P′PB=90°,可求∠APB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AB=AC.
(1)如图1,在△ADE中,若AD=AE,且∠DAE=∠BAC,求证:CD=BE;
(2)如图2,在△ADE中,若∠DAE=∠BAC=60°,且CD垂直平分AE,AD=3,CD=4,求BD的长;
(3)如图3,在△ADE中,当BD垂直平分AE于H,且∠BAC=2∠ADB时,试探究CD2,BD2,AH2之间的数量关系,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在军事上,常用时钟表示方向角(读数对应的时针方向),如正北为12点方向,北偏西30°为11点方向.在一次反恐演习中,甲队员在A处掩护,乙队员从A处沿12点方向以40米/分的速度前进,2分钟后到达B处.这时,甲队员发现在自己的1点方向的C处有恐怖分子,乙队员发现C处位于自己的2点方向(如图).假设距恐怖分子100米以外为安全位置.
(1)乙队员是否处于安全位置?为什么?
(2)因情况不明,甲队员立即发出指令,要求乙队员沿原路后撤,务必于15秒内到达安全位置.为此,乙队员至少应用多快的速度撤离?(结果精确到个位.参考数据:
 ,
, .)
.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=3a2b﹣2ab2+abc,小明同学错将“2A﹣B“看成”2A+B“,算得结果为4a2b﹣3ab2+4abc.
(1)计算B的表达式;
(2)求出2A﹣B的结果;
(3)小强同学说(2)中的结果的大小与c的取值无关,对吗?若a=
 ,b=
,b= ,
,求(2)中式子的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某检修小组从
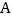 地出发,在南北方向的路上检修线路,如果规定向北行驶为正,向南行驶为负,一天行驶记录如下:(单位:千米)
地出发,在南北方向的路上检修线路,如果规定向北行驶为正,向南行驶为负,一天行驶记录如下:(单位:千米)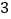 ,
,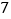 ,
,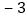 ,
,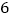 ,
,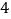 ,
,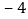 ,
,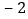 ,
,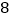 ,
,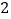 ,
,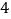 ,
,通过列式计算:
 收工时检修工人离
收工时检修工人离 地多远?在
地多远?在 地的哪个方向上?
地的哪个方向上? 若检修人员用的是耗油为每千米
若检修人员用的是耗油为每千米 升的汽车作交通工具,那么这天中,这辆汽车共耗油多少升?
升的汽车作交通工具,那么这天中,这辆汽车共耗油多少升? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(3)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请在坐标系中作出旋转中心S并写出旋转中心S的坐标:S
(4)在x轴上有一点P,使得PA+PB的值最小,请作图标出P点并写出点P的坐标.P . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,
 ,
, 的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,
的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点, ,垂足为G,若
,垂足为G,若 ,则AE的边长为
,则AE的边长为


A.
 B.
B.  C. 4 D. 8
C. 4 D. 8
相关试题

