【题目】同学们都知道:|5﹣(﹣2)|表示5与﹣2之差的绝对值,实际上也可理解为5与﹣2两数在数轴上所对应的两点之间的距离.请你借助数轴进行以下探索:
![]()
(1)数轴上表示5与﹣2两点之间的距离是 ,
(2)数轴上表示x与2的两点之间的距离可以表示为 .
(3)如果|x﹣2|=5,则x= .
(4)同理|x+3|+|x﹣1|表示数轴上有理数x所对应的点到﹣3和1所对应的点的距离之和,请你找出所有符合条件的整数x,使得|x+3|+|x﹣1|=4,这样的整数是 .
参考答案:
【答案】(1)7;(2)|x-2|;(3)7或-3;(4)-3、-2、-1、0、1;
【解析】
(1)根据数轴上两点之间的距离的表示方法即可得到结论;
(2)根据数轴上两点之间的距离的表示方法即可得到结论;
(3)利用绝对值求解即可;
(4)利用绝对值及数轴求解即可;
(1)数轴上表示5与-2两点之间的距离是|5-(-2)|=|5+2|=7,故答案为:7;
(2)数轴上表示x与2的两点之间的距离可以表示为|x-2|,故答案为:|x-2|;
(3)∵|x-2|=5,
∴x-2=5或x-2=-5,
解得:x=7或x=-3,
故答案为:7或-3;
(4)∵|x+3|+|x-1|表示数轴上有理数x所对应的点到-3和1所对应的点的距离之和,|x+3|+|x-1|=4,
∴这样的整数有-3、-2、-1、0、1,
故答案为:-3、-2、-1、0、1;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级(3)班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).

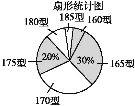
根据以上信息,解答下列问题:
(1)该班共有多少名学生?其中穿175型校服的学生有多少人?
(2)在条形统计图中,请把空缺的部分补充完整;
(3)在扇形统计图中,请计算185型校服所对应扇形圆心角的大小;
(4)求该班学生所穿校服型号的众数和中位数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物
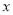 元(
元(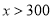 ).
).(1)请用含
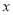 的代数式分别表示顾客在两家超市购物所付的费用;
的代数式分别表示顾客在两家超市购物所付的费用;(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由;
(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组对函数y=x+
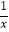 的图象和性质进行了探究,探究过程如下,请补充完整.
的图象和性质进行了探究,探究过程如下,请补充完整. x
…
﹣3
﹣2
﹣1
﹣

﹣



1
2
3
…
y
…
﹣
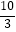
m
﹣2
﹣

﹣
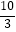
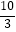

2

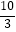
…
(1)自变量x的取值范围是 , m= .
(2)根据(1)中表内的数据,在如图所示的平面直角坐标系中描点,画出函数图象的一部分,请你画出该函数图象的另一部分.
(3)请你根据函数图象,写出两条该函数的性质;
(4)进一步探究该函数的图象发现: ①方程x+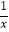 =3有个实数根;
=3有个实数根;
②若关于x的方程x+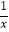 =t有2个实数根,则t的取值范围是 .
=t有2个实数根,则t的取值范围是 . 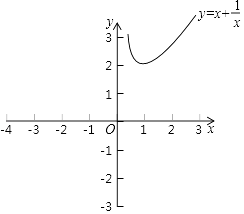
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“一带一路”战略的影响下,某茶叶经销商准备把“茶路”融入“丝路”,经计算,他销售10kgA级别和20kgB级别茶叶的利润为4000元,销售20kgA级别和10kgB级别茶叶的利润为3500元.
(1)求每千克A级别茶叶和B级别茶叶的销售利润;
(2)若该经销商一次购进两种级别的茶叶共200kg用于出口,其中B级别茶叶的进货量不超过A级别茶叶的2倍,请你帮该经销商设计一种进货方案使销售总利润最大,并求出总利润的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,等边三角形ABC的边长为5,点P在线段AB上,点D在线段BC上,且△PDE是等边三角形.
(1)初步尝试:若点P与点A重合时(如图1),BD+BE= .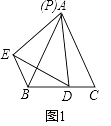
(2)类比探究:将点P沿AB方向移动,使AP=1,其余条件不变(如图2),试计算BD+BE的值是多少?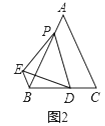
(3)拓展迁移:如图3,在△ABC中,AB=AC,∠BAC=70°,点P在线段AB的延长线上,点D在线段CB的延长线上,在△PDE中,PD=PE,∠DPE=70°,设BP=a,请直接写出线段BD、BE之间的数量关系(用含a的式子表示)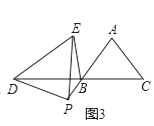
-
科目: 来源: 题型:
查看答案和解析>>【题目】在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:
“宇番2号”番茄挂果数量统计表
挂果数量x(个)
频数(株)
频率
25≤x<35
6
0.1
35≤x<45
12
0.2
45≤x<55
a
0.25
55≤x<65
18
b
65≤x<75
9
0.15
请结合图表中的信息解答下列问题:
(1)统计表中,a= ,b= ;
(2)将频数分布直方图补充完整;
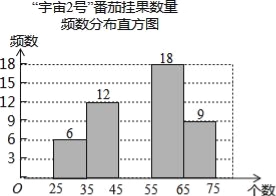
(3)若绘制“番茄挂果数量扇形统计图”,则挂果数量在“35≤x<45”所对应扇形的圆心角度数为 °;
(4)若所种植的“宇番2号”番茄有1000株,则可以估计挂果数量在“55≤x<65”范围的番茄有 株.
相关试题

