【题目】如图,已知平行四边形![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,
, ![]() 是
是![]() 延长线上的点,且
延长线上的点,且![]() 是等边三角形.
是等边三角形.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,求证:四边形
,求证:四边形![]() 是正方形.
是正方形.

参考答案:
【答案】见解析
【解析】试题分析:(1)根据对角线互相垂直的平行四边形是菱形.由题意易得△AOE≌△COE,∴∠AOE=∠COE=90°,∴BE⊥AC,∴四边形ABCD是菱形;
(2)根据有一个角是90°的菱形是正方形.由题意易得∠ADO=∠DAE+∠DEA=15°+30°=45°,∵四边形ABCD是菱形,∴∠ADC=2∠ADO=90°,∴四边形ABCD是正方形.
试题解析:证明:(1)∵四边形ABCD是平行四边形,
∴AO=CO.
又∵△ACE是等边三角形,
∴EO⊥AC(三线合一),即AC⊥BD,
∴四边形ABCD是菱形(对角线互相垂直的平行四边形是菱形).
(2)∵四边形ABCD是平行四边形,
∴AO=CO.
又∵△ACE是等边三角形,
∴EO平分∠AEC(三线合一),
∴∠AED=![]() ∠AEC=
∠AEC=![]() ×60°=30°,
×60°=30°,
又∵∠AED=2∠EAD
∴∠EAD=15°,
∴∠ADO=∠DAE+∠DEA=15°+30°=45°(三角形的一一个外角等于和它外角不相邻的两内角之和),
∵四边形ABCD是菱形,
∴∠ADC=2∠ADO=90°,
∴平行四边形ABCD是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列一组图形中点的个数的规律,第
 个图中点的个数是( )
个图中点的个数是( )
A. 49 B. 67 C. 88 D. 112
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.
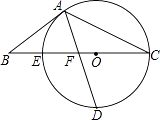
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF=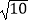 ,求⊙O的半径r及sinB.
,求⊙O的半径r及sinB. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.

(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是( )

A. ∠A+∠C+∠D+∠E=360°
B. ∠A+∠D=∠C+∠E
C. ∠A-∠C+∠D+∠E=180°
D. ∠E-∠C+∠D-∠A=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD是菱形,E是BD延长线上一点,F是DB延长线上一点,且DE=BF.请你以F为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可).

(1)连接 ;
(2)猜想: = ;
(3)证明:
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图(1),已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连结EB,过点A作AM⊥BE,垂足为M,AM交BD于点F.

(1)试说明OE=OF;
(2)如图(2),若点E在AC的延长线上,AM⊥BE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出说明理由;如果不成立,请说明理由.

相关试题

