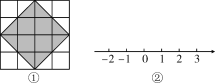
【题目】如图为4×4的网格(每个小正方形的边长均为1)与数轴.
(1)求出图①中阴影部分的面积;
(2)求出图①中阴影部分正方形的边长;
(3)在图②所示的数轴上作出表示![]() 的点A.
的点A.
参考答案:
【答案】(1) 8;(2)![]() (3)见解析.
(3)见解析.
【解析】
(1)由大正方形分成四个同样大小的小正方形,阴影部分为大正方形的四边中点的连线形成,所以阴影部分为大正方形面积的一半,根据正方形面积公式计算即可;
(2)由(1)的结论和正方形的面积公式易得到阴影部分正方形的边长;
(3)利用勾股定理在数轴上作直角边为2的等腰直角三角形,斜边的长即为![]() ,以O为圆心,以
,以O为圆心,以![]() 为半径画弧交数轴正半轴于一点,即为所求作的点.
为半径画弧交数轴正半轴于一点,即为所求作的点.
(1)阴影部分的面积=![]() 4×4=8;
4×4=8;
(2)设图①中阴影部分正方形的边长为a,则![]() ,
,
∴a=![]() ,
,
阴影部分正方形的边长为![]() ;
;
(3)在数轴上作边长为2的正方形,对角线的长为![]() ,以O为圆心,以
,以O为圆心,以![]() 为半径画弧交数轴正半轴于一点,即为所求作的点,如图所示:
为半径画弧交数轴正半轴于一点,即为所求作的点,如图所示: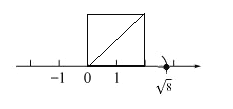
故答案为(1) 8;(2)![]() (3)见解析.
(3)见解析.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
⑴
 ;
;⑵
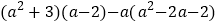 ;
;⑶
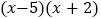 ;
; ⑷
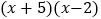 ;
;⑸
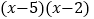 ;
;⑹
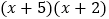 ;
; -
科目: 来源: 题型:
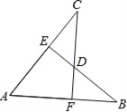
查看答案和解析>>【题目】如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④点C在AB的中垂线上.以上结论正确的有__________.(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应的括号内:
-11,
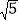 ,3,
,3,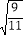 ,0,
,0,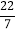 ,
,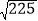 ,-12.101001…,-π,0.4.
,-12.101001…,-π,0.4.有理数{ …};
无理数{ ……};
正实数{ …};
负实数{ ……}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是_____________________;
(2)探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由;
(3)结论应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇与指挥中心O之间夹角∠EOF=70°,试求此时两舰艇之间的距离.
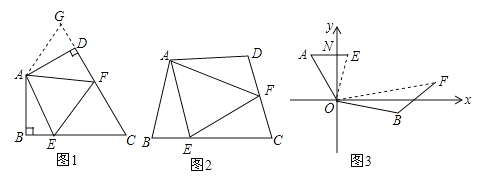
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点P(1,4)、Q(m,n)在函数y=
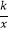 (x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积( )
(x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积( ) 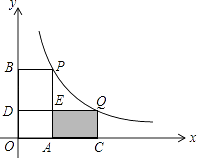
A.减小
B.增大
C.先减小后增大
D.先增大后减小
相关试题

