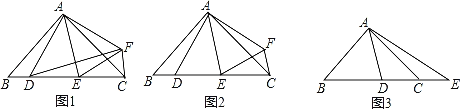
【题目】在△ABC中,AB=AC,∠BAC=2∠DAE=2α.
(1)如图1,若点D关于直线AE的对称点为F,求证:△ADF∽△ABC;
(2)如图2,在(1)的条件下,若α=45°,求证:DE2=BD2+CE2;
(3)如图3,若α=45°,点E在BC的延长线上,则等式DE2=BD2+CE2还能成立吗?请说明理由.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)成立,理由见解析.
【解析】试题分析:(1)根据轴对称的性质可得∠EAF=∠DAE,AD=AF,再求出∠BAC=∠DAF,然后根据两边对应成比例,夹角相等两三角形相似证明;
(2)根据轴对称的性质可得EF=DE,AF=AD,再求出∠BAD=∠CAF,然后利用“边角边”证明△ABD和△ACF全等,根据全等三角形对应边相等可得CF=BD,全等三角形对应角相等可得∠ACF=∠B,然后求出∠ECF=90°,最后利用勾股定理证明即可;
(3)作点D关于AE的对称点F,连接EF、CF,根据轴对称的性质可得EF=DE,AF=AD,再根据同角的余角相等求出∠BAD=∠CAF,然后利用“边角边”证明△ABD和△ACF全等,根据全等三角形对应边相等可得CF=BD,全等三角形对应角相等可得∠ACF=∠B,然后求出∠ECF=90°,最后利用勾股定理证明即可.
试题解析:(1)∵点D关于直线AE的对称点为F,
∴∠EAF=∠DAE,AD=AF,
又∵∠BAC=2∠DAE,
∴∠BAC=∠DAF,
∵AB=AC,
∴![]() ,
,
∴△ADF∽△ABC;
(2)∵点D关于直线AE的对称点为F,
∴EF=DE,AF=AD,
∵α=45°,
∴∠BAD=90°﹣∠CAD,
∠CAF=∠DAE+∠EAF﹣∠CAD=45°+45°﹣∠CAD=90°﹣∠CAD,
∴∠BAD=∠CAF,
在△ABD和△ACF中,

∴△ABD≌△ACF(SAS),
∴CF=BD,∠ACF=∠B,
∵AB=AC,∠BAC=2α,α=45°,
∴△ABC是等腰直角三角形,
∴∠B=∠ACB=45°,
∴∠ECF=∠ACB+∠ACF=45°+45°=90°,
在Rt△CEF中,由勾股定理得,EF2=CF2+CE2,
所以,DE2=BD2+CE2;
(3)DE2=BD2+CE2还能成立.
理由如下:作点D关于AE的对称点F,连接EF、CF,

由轴对称的性质得,EF=DE,AF=AD,
∵α=45°,
∴∠BAD=90°﹣∠CAD,
∠CAF=∠DAE+∠EAF﹣∠CAD=45°+45°﹣∠CAD=90°﹣∠CAD,
∴∠BAD=∠CAF,
由(2)得:CF=BD,∠ACF=∠B,
∵AB=AC,∠BAC=2α,α=45°,
∴△ABC是等腰直角三角形,
∴∠B=∠ACB=45°,
∴∠ECF=∠ACB+∠ACF=45°+45°=90°,
在Rt△CEF中,由勾股定理得,EF2=CF2+CE2,
所以,DE2=BD2+CE2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式x2+3x-5的值为2,则代数式-2x2-6x+14的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=-x+4与x轴、y轴分别交于A、B两点,直线BC与x轴、y轴分别交于C、B两点,连接BC,且
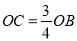 .
.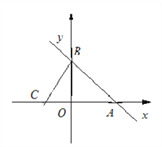
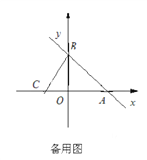

(1)求点A的坐标及直线BC的函数关系式;
(2)点M在x轴上,连接MB,当∠MBA+∠CBO=45°时,求点M的坐标;
(3)若点P在x轴上,平面内是否存在点Q,使点B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 射线比直线短 B. 两点确定一条直线
C. 经过三点只能作一条直线 D. 两点间的长度叫两点间的距离
-
科目: 来源: 题型:
查看答案和解析>>【题目】x=1是关于x的方程ax2+3x﹣5=0的一个解,则a的值是( )
A. ﹣2 B. ﹣1 C. 1 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题的个数是( )
①全等三角形的周长相等
②全等三角形的对应角相等
③全等三角形的面积相等
④面积相等的两个三角形全等.
A.4
B.3
C.2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件属于必然事件的是( )
A. 大家电视,正在播放新闻
B. 明天会下雨
C. 实数a<0,则2a<0
D. 掷一枚硬币,正面朝上
相关试题

