【题目】如图,已知A地在数轴上表示的数为-16,AB两地相距50个单位长度.小明从A地出发去B地,以每分钟2个单位长度的速度行进,第一次他向左1单位长度,第二次向右2单位长度,第三次再向左3单位长度,第四次又向右4单位长度…,按此规律行进.
![]()
(1)求出B地在数轴上表示的数;
(2)若B地在原点的右侧,经过第8次行进后小明到达点P,此时点P与点B相距几个单位长度?8次运动完成后一共经过了几分钟?
(3)若经过n次(n为正整数)行进后,小明到达点Q,请你直接写出:点Q在数轴上表示的数应如何表示?
参考答案:
【答案】(1)B地在数轴上表示的数为-66或34;(2)点P与点B相距46个单位长度,8次运动完成后一共经过了18分钟;(3)当n为奇数时,点Q表示的数为![]() ;当n为偶数时,点Q表示的数为
;当n为偶数时,点Q表示的数为![]() .
.
【解析】
(1)由题意可得B点位于A的左侧或右侧,AB两地相距50单位长度,A在数轴上表示的数为-16,据此可得B在数轴上表示的数;
(2)根据题意可以发现奇数次运动和偶数次运动是有规律的,从而得出第八次行进后到达点P,此时点P与B相距几个单位长度和八次运动完成后一共经过了几分;
(3)根据题意可以发现奇数次运动和偶数次运动是有规律的,从而可以写出n为偶数和奇数时,在数轴上Q表示的数是什么.
(1)-16-50=-66或-16+50=34
答:B地在数轴上表示的数为-66或34;
(2)∵B地在原点的右侧,∴B地在数轴上表示的数为34,
第8次运动到点P为![]() =-16+4=-12,
=-16+4=-12,
∴点P与点B相距的单位长度为34-(-12)=46,
8次运动完成后经过的时间为:(1+2+3+4+5+6+7+8)÷2=36÷2=18(分钟),
答:点P与点B相距46个单位长度,8次运动完成后一共经过了18分钟;
(3)第1次运动到点:-16-1,第2次为:-16+1,第3次为:-16+1-3=-16-2,
第4次为:-16+2,……照此规律:
当n为奇数时,点Q表示的数为![]() =
=![]() =
=![]() ;
;
当n为偶数时,点Q表示的数为![]()
-
科目: 来源: 题型:
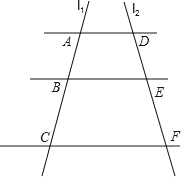
查看答案和解析>>【题目】如图,已知AD∥BE∥CF,它们以此交直线l1、l2于点A、B、C和D、E、F.若
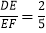 ,AC=14,
,AC=14,(1)求AB的长.
(2)如果AD=7,CF=14,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次安全知识测验中,学生得分均为整数,满分10分,这次测验中,甲,乙两组学生人数都为5人,成绩如下(单位:分):
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数
众数
中位数
甲
______________
8
8
乙
______________
9
______________
(2)已知甲组学生成绩的方差
 ,计算乙组学生成绩的方差,并说明哪组学生的成绩更稳定.
,计算乙组学生成绩的方差,并说明哪组学生的成绩更稳定. -
科目: 来源: 题型:
查看答案和解析>>【题目】
 为直线
为直线 上一点,以
上一点,以 为顶点作
为顶点作 ,射线
,射线 平分
平分
(1)如图①,
 与
与 的数量关系为______
的数量关系为______
(2)如图①,如果
 ,请你求出
,请你求出 的度数并说明理由;
的度数并说明理由;(3)若将图①中的
 绕点
绕点 旋转至图②的位置,
旋转至图②的位置, 依然平分
依然平分 ,若
,若 ,请直接写出
,请直接写出 的度数
的度数
-
科目: 来源: 题型:
查看答案和解析>>【题目】把四张形状大小完全相同的小正方形卡片(如图1)不重叠地放在一个底面为长方形(长为mcm,宽为ncm)的盒子的底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.则图2中两块阴影部分的周长和是( )

A. 4mcmB. 4ncmC. 2(m+n)cmD. 4(mn)cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司开发出一款新的节能产品,该产品的成本价为8元/件,该产品在正式投放市场前通过代销点进行了为期一个月30天的试销售,售价为13元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成如图所示的图象,图中的折线
 表示日销量
表示日销量 (件)与销售时间
(件)与销售时间 (天)之间的函数关系.
(天)之间的函数关系.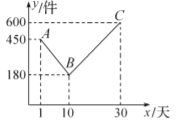
(1)直接写出
 与
与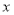 之间的函数解析式,并写出
之间的函数解析式,并写出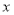 的取值范围.
的取值范围.(2)若该节能产品的日销售利润为
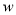 (元),求
(元),求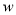 与
与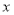 之间的函数解析式.日销售利润不超过1950元的共有多少天?
之间的函数解析式.日销售利润不超过1950元的共有多少天?(3)若
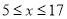 ,求第几天的日销售利润最大,最大的日销售利润是多少元?
,求第几天的日销售利润最大,最大的日销售利润是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】在体育测试时,初三的一名高个子男生推铅球,已知铅球所经过的路线是某二次函数图象的一部分(如图),若这个男生出手处A点的坐标为(0,2),铅球路线的最高处B点的坐标为B(6,5).
(1)求这个二次函数的表达式;
(2)该男生把铅球推出去多远?(精确到0.01米).

相关试题

