【题目】定义:对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x≥0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数.例如:一次函数y=x﹣1,它们的相关函数为y= .
.
(1)已知点A(﹣5,8)在一次函数y=ax﹣3的相关函数的图象上,求a的值;
(2)已知二次函数y=﹣x2+4x﹣![]() .
.
①当点B(m, ![]() )在这个函数的相关函数的图象上时,求m的值;
)在这个函数的相关函数的图象上时,求m的值;
②当﹣3≤x≤3时,求函数y=﹣x2+4x﹣![]() 的相关函数的最大值和最小值.
的相关函数的最大值和最小值.
参考答案:
【答案】(1)![]() ;(2)①m=2﹣
;(2)①m=2﹣![]() 或m=2+
或m=2+![]() 或m=2﹣
或m=2﹣![]() ;
;
②当﹣3≤x≤3时,函数y=﹣x2+4x﹣![]() 的相关函数的最大值为
的相关函数的最大值为![]() ,最小值为 ﹣
,最小值为 ﹣![]() .
.
【解析】试题分析:(1)函数![]() 的相关函数为
的相关函数为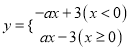 ,将点
,将点![]() 代入
代入![]() 求解即可.
求解即可.
(2)二次函数![]() 的相关函数为
的相关函数为 ,
,
![]() 分
分![]() 和
和![]() 两种情况,将点
两种情况,将点![]() 的坐标代入对应的关系式求解即可;
的坐标代入对应的关系式求解即可;
![]() 当
当![]() 时,
时, ![]() ,然后求得此时的最大值,当
,然后求得此时的最大值,当![]() 时,函数
时,函数![]() ,求得此时的最大值和最小值,从而可得出当
,求得此时的最大值和最小值,从而可得出当![]() 时,函数
时,函数![]() 的相关函数的最大值和最小值。
的相关函数的最大值和最小值。
试题解析:(1)![]() 的相关函数
的相关函数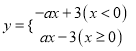 ,将
,将![]() 代入
代入![]() 得:
得: ![]() ,
,
解得![]() .
.
(2)二次函数![]() 的相关函数为
的相关函数为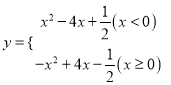
①当![]() 时,将
时,将![]() 代入
代入![]() ,
,
得![]()
解得: ![]() (舍去)或
(舍去)或![]() .
.
当![]() 时,将
时,将![]() 代入
代入![]() 得:
得: ![]()
解得: ![]() 或
或![]() .
.
综上所述:m=2﹣![]() 或m=2+
或m=2+![]() 或m=2﹣
或m=2﹣![]() .
.
②当![]() 时,
时, ![]() 抛物线的对称轴为
抛物线的对称轴为![]()
此时![]() 随
随![]() 的增大而减小,∴此时
的增大而减小,∴此时![]() 的最大值为
的最大值为![]() .
.
当![]() 时,函数
时,函数![]() 抛物线的对称轴为
抛物线的对称轴为![]() 当
当![]() 有最小值,最小值为﹣
有最小值,最小值为﹣![]() ,当
,当![]() 时,有最大值,最大值
时,有最大值,最大值![]()
综上所述,当![]() 时,函数
时,函数![]() 的相关函数的最大值为
的相关函数的最大值为![]() ,
,
最小值为 ﹣![]() ;
;
-
科目: 来源: 题型:
查看答案和解析>>【题目】盐城市大力发展绿色交通,构建公共绿色交通体系,“共享单车”的投入使用给人们的出行带来便利,小明随机调查了若干市民租用共享单车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如图所示的统计图,请根据图中信息,解答下列问题:

(1)这次被调査的总人数是 ;
(2)补全条形统计图;
(3)在扇形统计图中,求表示A组(t≤10分)的扇形圆心角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备租用一批汽车,现有甲、乙两种客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人.已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.求1辆甲种客车和1辆乙种客车的租金分别是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠B=90°,AD∥BC,BC=2AD,点E为边BC的中点.
(1)求证:四边形AECD为平行四边形;
(2)在CD边上取一点F,联结AF、 AC、 EF,设AC与EF交于点G,且∠EAF=∠CAD.
求证:△AEC∽△ADF;
(3)在(2)的条件下,当∠ECA=45°时.求:
 的比值.
的比值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“双剑合璧,天下无敌”,其意思是指两个人合在一起,取长补短,威力无比.在二次根式中也常有这种相辅相成的“对子”,如:
 ,
,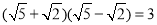 ,它们的积中不含根号,我们说这两个二次根式是互为有理化因式,其中一个是另一个的有理化因式,于是,二次根式除法可以这样解:
,它们的积中不含根号,我们说这两个二次根式是互为有理化因式,其中一个是另一个的有理化因式,于是,二次根式除法可以这样解: ,
, .
.像这样通过分子、分母同乘一个式子把分母中的根号化去的方法,叫做分母有理化.
解决下列问题:
(1)将
 分母有理化得 ;
分母有理化得 ; 的有理化因式是 ;
的有理化因式是 ;(2)化简:
 = ;
= ;(3)化简:
 ……+
……+ .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了保护环境,某企业决定购买10台污水处理设备;现有A、B两种型号的设备,其中每台的价格、月处理污水量及年消耗费如下表:
A型
B型
价格(万元/台)
12
10
处理污水量(吨/月)
240
200
年消耗费(万元/台)
1
1
经预算,该企业购买设备的资金不高于105万元。
(1) 请你设计该企业有几种购买方案;
(2)若该企业每月产生的污水量为2040吨,为了节约资金,应选择哪种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A(6,0),C(0,4)点D与坐标原点O重合,动点P从点O出发,以每秒2个单位的速度沿O﹣A﹣B﹣C的路线向终点C运动,连接OP、CP,设点P运动的时间为t秒,△CPO的面积为S,下列图象能表示t与S之间函数关系的是( )

A.
B.

C.

D.

相关试题

