【题目】如图,四边形ABCD中,AD=CD,∠DAB=∠ACB=90°,过点D作DE⊥AC,垂足为F,DE与AB相交于点E.
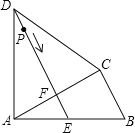
(1)求证:ABCF=CBCD;
(2)已知AB=15,BC=9,P是射线DE上的动点,设DP=x(x>0),四边形BCDP的面积为y.
①求y关于x的函数关系式;
②当PB+PC最小时,求x,y的值.
参考答案:
【答案】(1)见解析;(2)①y=![]() (x+9)×6=3x+27(x>0);②x=
(x+9)×6=3x+27(x>0);②x=![]() ,此时y=
,此时y=![]() .
.
【解析】
试题分析:(1)首先证得△DCF∽△ABC,利用相似三角形的性质可得结论;
(2)①由勾股定理可得BC的长,利用梯形的面积公式可得结果;②首先由垂直平分线的性质可得点C关于直线DE的对称点是点A,PB+PC=PB+PA,故只要求PB+PA最小即可,因为当P、A、B三点共线时PB+PA最小,由中位线的性质可得EF=![]() ,由(1)知CF:BC=CD:AB,可得CD,即得AD,在Rt△ADF中,由勾股定理可得DF,易得DE,即得x,代入①可得y.
,由(1)知CF:BC=CD:AB,可得CD,即得AD,在Rt△ADF中,由勾股定理可得DF,易得DE,即得x,代入①可得y.
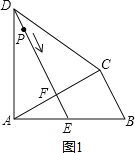
(1)证明:如图1,∵AD=CD,DE⊥AC,
∴DE垂直平分AC,
∴AF=CF,∠DFA=∠DFC=90°,∠DAF=∠DCF,
∵∠DAB=∠DAF+∠CAB=90°,∠CAB+∠B=90°,
∴∠DCF=∠DAF=∠B,
在Rt△DCF和Rt△ABC中,∠DFC=∠ACB=90°,∠DCF=∠B,
∴△DCF∽△ABC,
∴![]() ,
,
∴ABCF=CBCD;
(2)解:①∵AB=15,BC=9,∠ACB=90°,
∴AC=![]() =
=![]() =12,
=12,
∴CF=AF=6,
∴y=![]() (x+9)×6=3x+27(x>0);
(x+9)×6=3x+27(x>0);
②由(1)知点C关于直线DE的对称点是点A,
∴PB+PC=PB+PA,故只要求PB+PA最小,显然当P、A、B三点共线时PB+PA最小,
此时DP=DE,PB+PA=AB,
∵EF∥BC,∴EF=![]() ,
,
∵CF:BC=CD:AB,即6:9=CD:15,
∴CD=10=AD,
Rt△ADF中,AD=10,AF=6,
∴DF=8,
∴DE=DF+EF=8+![]() =
=![]() ,
,
∴x=![]() ,此时y=
,此时y=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=α(30°<α<45°),∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.
(1)如图,当α=40°,且射线OM在∠AOB的外部时,用直尺、量角器画出射线OD,ON的准确位置;
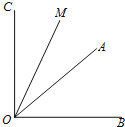
(2)求(1)中∠MON的度数,要求写出计算过程;
(3)当射线OM在∠AOB的内部时,用含α的代数式表示∠MON的度数.(直接写出结果即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂去年的产值是a万元,今年比去年增加10%,今年的产值是 万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:等边△ABC的边长为2,点D为平面内一点,且BD=
 AD=2
AD=2 ,则CD= .
,则CD= . -
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:ax﹣ay= .
-
科目: 来源: 题型:
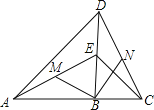
查看答案和解析>>【题目】如图,已知点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点,现有如下结论:①∠ABD=∠BDN;②MB=NB;③MB⊥NB;④S△ABM=S△BCN,其中正确的结论是 (只填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:线段AB=20cm.
(1)如图1,点P沿线段AB自A点向B点以2厘米/秒运动,点P出发2秒后,点Q沿线段BA自B点向A点以3厘米/秒运动,问再经过几秒后P、Q相距5cm?
(2)如图2:AO=4cm,PO=2cm,∠POB=60°,点P绕着点O以60度/秒的速度逆时针旋转一周停止,同时点Q沿直线BA自B点向A点运动,假若点P、Q两点能相遇,求点Q运动的速度.
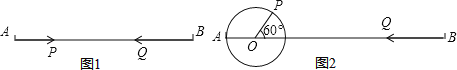
相关试题

