【题目】已知:等边△ABC的边长为2,点D为平面内一点,且BD=![]() AD=2
AD=2![]() ,则CD= .
,则CD= .
参考答案:
【答案】2或4
【解析】
试题分析:①根据等腰三角形的性质,可得DE的长,根据正弦函数,可得∠CAD的度数,根据等边三角形,可得CD的长;
②根据等腰三角形的性质,可得DE的长,根据正弦函数,可得∠EAD的度数,根据角的和差,可得A、C、D在同一条直线上,根据线段的和差,可得答案.
解:如图1:
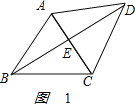
由BD=![]() AD=2
AD=2![]() ,得
,得
AD=AB=AC=2.
由等腰三角形的性质,得
DE=![]() .
.
sin∠DAE=![]() ,
,
∠DAE=60°,△ACD是等边三角形,
CD=AC=2;
如图2:
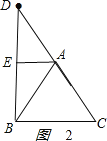 ,
,
由BD=![]() AD=2
AD=2![]() ,得
,得
AD=AB=AC=2.
由等边三角形的性质,得
DE=![]() ,∠DAE=∠BAE.
,∠DAE=∠BAE.
sin∠DAE=![]() ,
,
∠DAE=∠BAE=60°,
AD与AC在同一条直线上,
CD=AC=2;
CD=AD+AC=2+2=4.
故答案为:2或4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB是⊙O的直径,AB=6,点C,D在⊙O上,且CD平分∠ACB,∠CAB=60°.
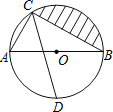
(1)求BC及阴影部分的面积;
(2)求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=α(30°<α<45°),∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.
(1)如图,当α=40°,且射线OM在∠AOB的外部时,用直尺、量角器画出射线OD,ON的准确位置;
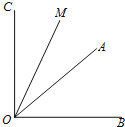
(2)求(1)中∠MON的度数,要求写出计算过程;
(3)当射线OM在∠AOB的内部时,用含α的代数式表示∠MON的度数.(直接写出结果即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂去年的产值是a万元,今年比去年增加10%,今年的产值是 万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AD=CD,∠DAB=∠ACB=90°,过点D作DE⊥AC,垂足为F,DE与AB相交于点E.
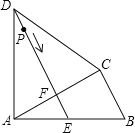
(1)求证:ABCF=CBCD;
(2)已知AB=15,BC=9,P是射线DE上的动点,设DP=x(x>0),四边形BCDP的面积为y.
①求y关于x的函数关系式;
②当PB+PC最小时,求x,y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:ax﹣ay= .
-
科目: 来源: 题型:
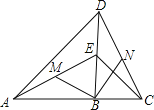
查看答案和解析>>【题目】如图,已知点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点,现有如下结论:①∠ABD=∠BDN;②MB=NB;③MB⊥NB;④S△ABM=S△BCN,其中正确的结论是 (只填序号).
相关试题

