【题目】已知:线段AB=20cm.
(1)如图1,点P沿线段AB自A点向B点以2厘米/秒运动,点P出发2秒后,点Q沿线段BA自B点向A点以3厘米/秒运动,问再经过几秒后P、Q相距5cm?
(2)如图2:AO=4cm,PO=2cm,∠POB=60°,点P绕着点O以60度/秒的速度逆时针旋转一周停止,同时点Q沿直线BA自B点向A点运动,假若点P、Q两点能相遇,求点Q运动的速度.
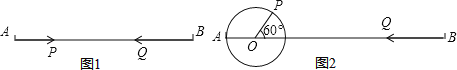
参考答案:
【答案】(1)经过![]() s或
s或![]() s后,点P、Q相距5cm.(2)点Q的速度为9cm/s或2.8cm/s.
s后,点P、Q相距5cm.(2)点Q的速度为9cm/s或2.8cm/s.
【解析】
试题分析:(1)设经过xs,P、Q两点相距5cm,分相遇前和相遇后两种情况建立方程求出其解即可;
(2)由于点P,Q只能在直线AB上相遇,而点P旋转到直线AB上的时间分两种情况,所以根据题意列出方程分别求解.
解:(1)设再经过ts后,点P、Q相距5cm,
①P、Q未相遇前相距5cm,依题意可列
2(t+2)+3t=20﹣5,解得,t=![]() ,
,
②P、Q相遇后相距5cm,依题意可列
2(t+2)+3t=20+5,解得,t=![]() ,
,
答:经过![]() s或
s或![]() s后,点P、Q相距5cm.
s后,点P、Q相距5cm.
(2)点P,Q只能在直线AB上相遇,则点P旋转到直线AB上的时间为![]() =2s
=2s
或![]()
设点Q的速度为ym/s,
当2秒时相遇,依题意得,2y=20﹣2=18,解得y=9
当5秒时相遇,依题意得,5y=20﹣6=14,解得y=2.8
答:点Q的速度为9cm/s或2.8cm/s.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AD=CD,∠DAB=∠ACB=90°,过点D作DE⊥AC,垂足为F,DE与AB相交于点E.
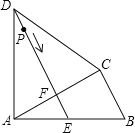
(1)求证:ABCF=CBCD;
(2)已知AB=15,BC=9,P是射线DE上的动点,设DP=x(x>0),四边形BCDP的面积为y.
①求y关于x的函数关系式;
②当PB+PC最小时,求x,y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:ax﹣ay= .
-
科目: 来源: 题型:
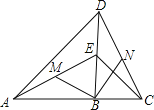
查看答案和解析>>【题目】如图,已知点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点,现有如下结论:①∠ABD=∠BDN;②MB=NB;③MB⊥NB;④S△ABM=S△BCN,其中正确的结论是 (只填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三家超市为了促销一种定价相同的商品,甲超市先降价20%,后又降价10%;乙超市连续两次降价15%;丙超市一次降价30%。那么顾客到__________家超市购买这种商品更合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:a2+ab= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标中,已知四边形ABCD是正方形,点A在原点,点B的坐标是(3,1),则点D的坐标是 .

相关试题

