【题目】如图,已知E、F为平行四边形ABCD的对角线上的两点,且BE=DF,∠AEC=90°.求证:四边形AECF为矩形. 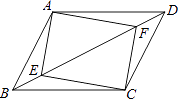
参考答案:
【答案】证明:连接AC交BD于O,如图所示: ∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵BE=DF,
OE=OF.
∵OA=OC,
∴AECF是平行四边形;
∵∠AEC=90°,
∴四边形AECF为矩形.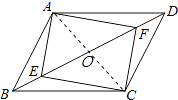
【解析】连接AC交BD于O,由平行四边形的性质得出OA=OC,OB=OD,由已知条件得出OE=OF,证出四边形AECF为平行四边形,再由∠AEC=90°,即可得出结论.
【考点精析】利用平行四边形的性质和矩形的判定方法对题目进行判断即可得到答案,需要熟知平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:S1=1+
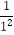 +
+ 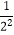 ,S2=1+
,S2=1+ 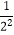 +
+ 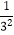 ,S3=1+
,S3=1+ 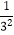 +
+ 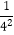 ,S4=1+
,S4=1+ 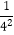 +
+ 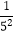 ,S5=1+
,S5=1+ 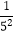 +
+ 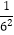 ,…则
,…则 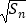 =(用含n的代数式表示,其中n为正整数)
=(用含n的代数式表示,其中n为正整数) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c满足|a﹣
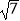 |+
|+  +(c﹣4
+(c﹣4 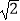 )2=0.
)2=0.
(1)求a、b、c的值;
(2)判断以a、b、c为边能否构成三角形?若能构成三角形,此三角形是什么形状?并求出三角形的面积;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从热气球C处测得地面A、B两点的俯角分别为45°、30°,如果此时热气球C处离地面的高度CD为100米,且点A、D、B在同一直线上,求AB两点间的距离(结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为扩大销售,尽快减少库存,商场决定釆取降价措施,调查发现,每件衬衫,每降价1元,平均每天可多销售2件,若商场每天要盈利1200元,每件衬衫应降价( )
A. 5元 B. 10元 C. 20元 D. 10元或20元
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动
(1)情境观察
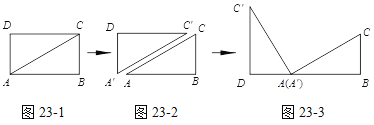
将矩形纸片ABCD沿对角线AC剪开,得到△ABC和△A′C′D,如图23-1所示.将△A′C′D的顶点A′与点A重合,并绕点A(A′)按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图23-2所示.
观察图23-2可知:与BC相等的线段是 ,∠CAC′= 度.
(2)问题探究
如图23-3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.
(3)拓展延伸
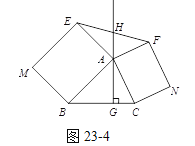
如图23-4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB=k·AE,AC=k·AF,试探究HE与HF之间的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 3a3·2a2=6a6 B. 3x·3x4=9x4
C. 2x3·4x5=8x8 D. 5b7·5b7=10b14
相关试题

