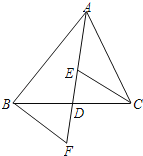
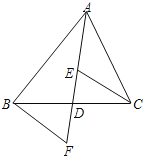
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法:
①△ABD和△ACD面积相等;
②∠BAD=∠CAD;
③△BDF≌△CDE;
④BF∥CE;
⑤CE=AE.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
参考答案:
【答案】C.
【解析】
试题分析:①∵AD是△ABC的中线,∴BD=CDF,∴△ABD和△ACD面积相等;故①正确;
②若在△ABC中,当AB≠AC时,AD不是∠BAC的平分线,即∠BAD≠∠CAD.即②不一定正确;
③∵AD是△ABC的中线,∴BD=CD,
在△BDF和△CDE中,∵BD=CD,∠BDF=∠CDE,DF=DE,∴△BDF≌△CDE(SAS).故③正确;
④∵△BDF≌△CDE,∴∠CED=∠BFD,∴BF∥CE;故④正确;
⑤∵△BDF≌△CDE,∴CE=BF,∴只有当AE=BF时,CE=AE.故⑤不一定正确.
综上所述,正确的结论是:①③④,共有3个.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(3,y1),B(﹣2,y2)在抛物线y=x2﹣5x上,则y1y2 . (填“>”,“<”或“=”)
-
科目: 来源: 题型:
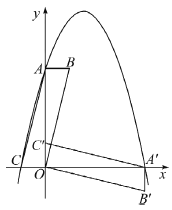
查看答案和解析>>【题目】在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
(1)若抛物线过点C、A、A′,求此抛物线的解析式;
(2)点M是第一象限内抛物线上的一动点,问:当点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时M的坐标;
(3)若P为抛物线上的一动点,N为x轴上的一动点,点Q坐标为(1,0),当P、N、B、Q 构成平行四边形时,求点P的坐标,当这个平行四边形为矩形时,求点N的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的
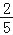 ,求横、竖彩条的宽度.
,求横、竖彩条的宽度.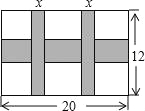
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.
(1)求证:BD=CE;
(2)求证:∠M=∠N.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)当a=2,b=
 时,分别求代数式(ab)2和a2-2ab+b2的值.
时,分别求代数式(ab)2和a2-2ab+b2的值.(2)当a=1,b=5时,分别求代数式(ab)2和a2-2ab+b2的值;
(3)观察(1)(2)中代数式的值,a2-2ab+b2与(ab)2有何关系?
(4)利用你发现的规律,求135.72-2×135.7×35.7+35.72的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,①调查本班同学的视力;②调查一批节能灯管的使用寿命;③为保证“神舟9号”的成功发射,对其零部件进行检查;④对乘坐某班次客车的乘客进行安检.其中适合采用抽样调查的是( )
A.① B.② C.③ D.④
相关试题

