【题目】如图(1)在Rt△ABC中,∠C=90°,AB=5cm.BC=a cm,AC=3cm,且a是方程x2﹣(m﹣1)x+m+4=0的根.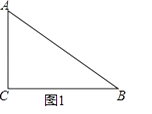
(1)求a和m的值;
(2)如图(2),有一个边长为 ![]() 的等边三角形DEF从C出发,以1cm/s的速度沿CB方向移动,至△DEF全部进入与△ABC为止,设移动时间为xs,△DEF与△ABC重叠部分面积为y,试求出y与x的函数关系式并注明x的取值范围;
的等边三角形DEF从C出发,以1cm/s的速度沿CB方向移动,至△DEF全部进入与△ABC为止,设移动时间为xs,△DEF与△ABC重叠部分面积为y,试求出y与x的函数关系式并注明x的取值范围;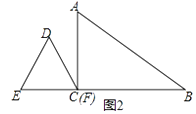
(3)试求出发后多久,点D在线段AB上?
参考答案:
【答案】
(1)
解:在Rt△ABC中,∠C=90°,AB=5cm.BC=a cm,AC=3cm,
根据勾股定理可得,BC=4cm,即a=4.
∵a是方程x2﹣(m﹣1)x+m+4=0的根
∴42﹣(m﹣1)×4+m+4=0的根,
∴m=8,
(2)
解:由(1)得a=4,则等边三角形DEF的边长为 ![]() =2(cm),
=2(cm),
如图(1),

当0≤x≤1时,易知∠DFC=60°,
∵∠ACF=90°,
∴∠CGF=30°,
∴CG= ![]() CF=
CF= ![]() x
x
∴y=S△CGF= ![]() CFCG=
CFCG= ![]() x
x ![]() x=
x= ![]() x2,
x2,
如图(2),
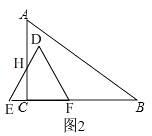
当1<x≤2时,BE=2﹣x,HC= ![]() EC=
EC= ![]() (2﹣x),
(2﹣x),
∴S△HEC= ![]() ECHC=
ECHC= ![]() (2﹣x)
(2﹣x) ![]() (2﹣x)=
(2﹣x)= ![]() (2﹣x)2,
(2﹣x)2,
∴y=S△DEF﹣S△HEC= ![]() ×22﹣
×22﹣ ![]() (2﹣x)2=﹣
(2﹣x)2=﹣ ![]() x2+2
x2+2 ![]() x﹣
x﹣ ![]()
综上, 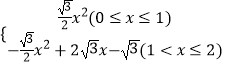
(3)
解:如图(3),

若点D在线段AB上,
过点D作DM⊥BC于点M,此时DM∥AC,
∴△BDM∽△BAC
∴ ![]() 即
即 ![]() ,
,
∴DM= ![]()
又等边三角形DEF的边长2,
∴DM= ![]()
∴ ![]() ,
,
∴x= ![]()
即出发后 ![]() s时,点D在线段AB上.
s时,点D在线段AB上.
【解析】(1)先利用勾股定理求出a,再用一元二次方程的解求出m;(2)分两种情况①利用三角形的面积公式,②利用三角形的面积差即可得出结论;(3)先判断出△BDM∽△BAC再用DM建立方程求解即可.
【考点精析】通过灵活运用三角形的面积和相似三角形的性质,掌握三角形的面积=1/2×底×高;对应角相等,对应边成比例的两个三角形叫做相似三角形即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.
(1)依题意补全图形;(2)若∠PAC=20°,求∠AEB的度数;
(3)连结CE,写出AE, BE, CE之间的数量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
 (x>0)的图象交于A(2,﹣1),B(
(x>0)的图象交于A(2,﹣1),B(  ,n)两点,直线y=2与y轴交于点C.
,n)两点,直线y=2与y轴交于点C. 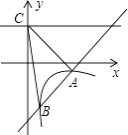
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.
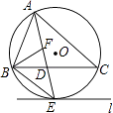
(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】周末小石去博物馆参加综合实践活动,乘坐公共汽车0.5小时后想换乘另一辆公共汽车,他等候一段时间后改为利用手机扫码骑行摩拜单车前往.已知小石离家的路程s(单位:千米)与时间t(单位:小时)的函数关系的图象大致如图.则小石骑行摩拜单车的平均速度为( )

A.30千米/小时
B.18千米/小时
C.15千米/小时
D.9千米/小时 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列例题
解方程:|x|+|2x﹣1|=5.
解:①当x≥0.5时,原方程可化为:x+2x﹣1=5,它的解是x=2;
②当0≤x<0.5时,原方程可化为:x﹣2x+1=5,解之,得x=﹣4,
经检验x不合题意,舍去.
③当x<0时,原方程可化为:﹣x﹣2x+1=5,它的解是x=﹣
 .
.所以原方程的解是x=2或x=﹣
 .
.(1)根据上面的解题过程,写出方程2|x﹣1|﹣x=4的解.
(2)根据上面的解题过程,解方程:2|x﹣1|﹣|x|=4.
(3)方程|x|﹣2|x﹣1|=4是否有解.
-
科目: 来源: 题型:
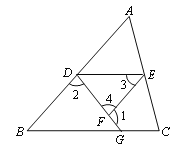
查看答案和解析>>【题目】如图, 已知∠1+∠2=180o, ∠3=∠B, 试说明∠DEC+∠C=180o. 请完成下列填空:
解:∵∠1+∠2=180o(已知)
又∵∠1+ =180o(平角定义)
∴∠2= (同角的补角相等)
∴ (内错角相等,两直线平行)
∴∠3 = (两直线平行,内错角相等)
又∵∠3=∠B(已知)
∴ (等量代换)
∴ ∥ ( )
∴∠DEC+∠C=180o( )
相关试题

