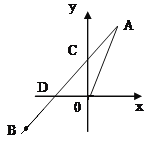
【题目】如图正比例函数y=2x的图像与一次函数 ![]() 的图像交于点A(m,2),一次函数的图象经过点B(-2,-1)与y轴交点为C与x轴交点为D.
的图像交于点A(m,2),一次函数的图象经过点B(-2,-1)与y轴交点为C与x轴交点为D.
(1)求一次函数的解析式;
(2)求![]() 的面积。
的面积。
参考答案:
【答案】(1)一次函数的解析式为![]() ;(2)1.
;(2)1.
【解析】(1)首先根据正比例函数解析式求得m的值,再进一步运用待定系数法求得一次函数的解析式;
(2)根据(1)中的解析式,令y=0求得点C的坐标,从而求得三角形的面积.
解:(1)由题可得,把点A(m,2)代入正比例函数y=2x 得
2=2m
m=1
所以点A(1,2)
因为一次函数图象又经过点B(-2,-1),所以
![]()
解方程组得![]()
这个一次函数的解析式为![]()
(2)因为一次函数图象与x轴的交点为D,
所以点D的坐标为(-1,0)
因为![]() 的底为OD=1,高为A点的纵坐标2
的底为OD=1,高为A点的纵坐标2
所以![]()
“点睛”此题综合考查了待定系数法求函数解析式、直线与坐标轴的交点的求法,关键是根据正比例函数解析式求得m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明帮助小芳荡秋千(如图1),在小明的助推下,秋千越来越高,秋千离地面的高度
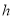 (
(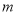 )与摆动时间
)与摆动时间 (
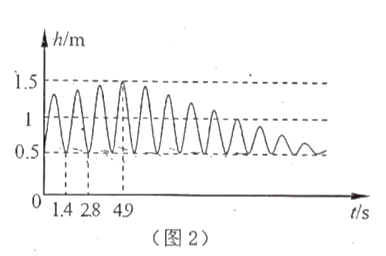
(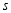 )之间的关系如图2所示.
)之间的关系如图2所示.(1)根据函数定义,请判断变量
 是否为关于
是否为关于 的函数?
的函数?(2)结合图象回答:
①秋千静止时离地面的距离是多少?秋千的最高点与地面距离是多少?
②多长时间后小明就不再推小芳?
③从最低点开始向前和向后,再反悔到最低点,这叫做一个周期,请问,小芳完成第一个周期用了多长时间?
④每个周期的时间都是相等的,经过多长时间,秋千的最高点是1m?

-
科目: 来源: 题型:
查看答案和解析>>【题目】中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:
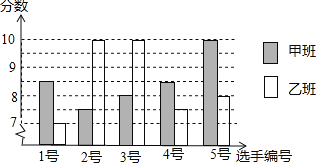
 根据上图填写下表:
根据上图填写下表:平均数
中位数
众数
方差
甲班
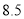

______
______
乙班

______
10

 根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好.
根据上表数据,分别从平均数、中位数、众数、方差的角度分析哪个班的成绩较好. -
科目: 来源: 题型:
查看答案和解析>>【题目】有下列说法:①如果一个数的立方根等于它本身,那么它一定是1戓0:②无限小数都是无理数;③实数与数轴上的点一一对应;④
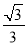 是分数;③近似数5.60所表示的准确数的范围是:5.55≤x<5.65.其中正确的个数是( )
是分数;③近似数5.60所表示的准确数的范围是:5.55≤x<5.65.其中正确的个数是( )A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上标出的所有点中,任意相邻两点间的距离相等,已知点A表示﹣12,点G表示6.
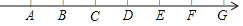
(1)表示原点的点是 ,点C表示的数是 ;
(2)数轴上有两点M、N,点M到点D的距离为
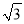 ,点N到点D的距离为4,求点M,N之间的距离;
,点N到点D的距离为4,求点M,N之间的距离;(3)点P为数轴上一点,且表示的数是整数,点P到点A的距离与点P到点G的距离之和为18,则这样的点P有 个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,已知直线AB的函数解析式为y=﹣2x+8,与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接EF,问:
①若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围;
②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是小亮同学设计的一个轴对称图形的一部分,其中点
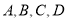 都在直角坐标系网格的格点上,每个小正方形的边长都等于1.
都在直角坐标系网格的格点上,每个小正方形的边长都等于1.(1)请画出关于
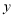 轴成轴对称图形的另一半,并写出
轴成轴对称图形的另一半,并写出 两点的对应点坐标.
两点的对应点坐标.(2)记
 两点的对应点分别为
两点的对应点分别为 ,请直接写出封闭图形
,请直接写出封闭图形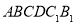 的面积.
的面积.
相关试题

