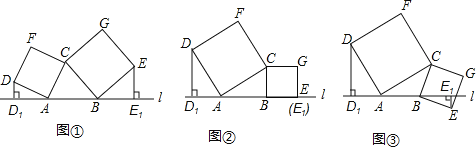
【题目】如图①所示,已知A、B为直线l上两点,点C为直线l上方一动点,连接AC、BC,分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG,过点D作DD1⊥l于点D1,过点E作EE1⊥l于点E1.
(1)如图②,当点E恰好在直线l上时(此时E1与E重合),试说明DD1=AB;
(2)在图①中,当D、E两点都在直线l的上方时,试探求三条线段DD1、EE1、AB之间的数量关系,并说明理由;
(3)如图③,当点E在直线l的下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系.(不需要证明)
参考答案:
【答案】(1)证明详见解析;(2)AB=DD1+EE1;(3)AB=DD1-EE1.
【解析】试题分析:(1)由四边形CADF、CBEG是正方形可得AD=CA,∠DAC=∠ABC=90°,又由同角的余角相等,求得∠ADD1=∠CAB,然后利用AAS证得△ADD1≌△CAB,根据全等三角形的对应边相等,即可得DD1=AB;
(2)首先过点C作CH⊥AB于H,由DD1⊥AB,可得∠DD1A=∠CHA=90°,由四边形CADF是正方形,可得AD=CA,又由同角的余角相等,求得∠ADD1=∠CAH,然后利用AAS证得△ADD1≌△CAH,根据全等三角形的对应边相等,即可得DD1=AH,同理EE1=BH,则可得AB=DD1+EE1;
(3)证明方法同(2),即可得到AB=DD1-EE1.
试题解析:(1)因为四边形CADF、CBEG是正方形,
所以AD=CA,∠DAC=∠ABC=90°,
所以∠DAD1+∠CAB=90°,
因为DD1⊥AB,
所以∠DD1A=∠ABC=90°,
所以∠DAD1+∠ADD1=90°,
所以∠ADD1=∠CAB,
在△ADD1和△CAB中,
∠ADD1=∠CAB,∠DD1A=∠ABC ,AD=CA,
所以△ADD1≌△CAB,
所以DD1=AB;
(2)AB=DD1+EE1,理由如下:
过点C作CH⊥AB于H ,与(1)同理,△ADD1≌△CAH,所以DD1=AH,同理EE1=BH,所以AB=DD1+EE1;
(3)AB=DD1-EE1,理由如下:
过点C作CH⊥AB于H ,与(1)同理,△ADD1≌△CAH,所以DD1=AH,同理EE1=BH,所以AB=DD1-EE1.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某自治州自然风景优美,每天吸引大量游客前来游览,经统计,某段时间内来该州风景区游览的人数约为36000人,用科学记数法表示36000为( )
A.36×103
B.0.36×106
C.0.36×104
D.3.6×104 -
科目: 来源: 题型:
查看答案和解析>>【题目】根据下面给出的数轴,解答下面的问题:
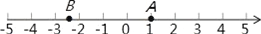
(1)请根据图中A、B两点的位置,分别写出它们所表示的有理数A:__ B:__;
(2)观察数轴,与点A的距离为4的点表示的数是:__;
(3)若将数轴折叠,使得A点与﹣3表示的点重合,则B点与数__表示的点重合;
(4)若数轴上M、N两点之间的距离为2018(点M在点N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M:__ N:__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个数加上﹣12得﹣5,那么这个数为( )
A. 17 B. 7 C. ﹣17 D. ﹣7
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2-8x-1=0配方后可变形为( ).
A.(x+4)2=17 B.(x+4)2=15 C.(x-4)2=17 D.(x-4)2=15
-
科目: 来源: 题型:
查看答案和解析>>【题目】用计算器计算并填空:
①11-2=______=(3)2;
②1 111-22=______=(33)2;
③111 111-222=_________=(333)2;
④11 111 111-2 222=_______=(3 333)2.
根据你发现的规律计算:
_____________-222 222=(333 333)2.
-
科目: 来源: 题型:
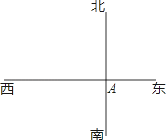
查看答案和解析>>【题目】小明从A点出发向北偏东60°方向走了80m米到达B地,从B地他又向西走了160m到达C地.
(1)用1:4000的比例尺(即图上1cm等于实际距离40m)画出示意图,并标上字母;
(2)用刻度尺出AC的距离(精确到0.01cm),并求出C但距A点的实际距离(精确到1m);
(3)用量角器测出C点相对于点A的方位角.
相关试题

