【题目】在正方形网格中建立如图所示的平面直角坐标系xOy.△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:
(1)将△ABC向下平移5个单位长度,画出平移后的A1B1C1,并写出点A的对应点A1的坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)将△ABC绕点C逆时针旋转90°,画出旋转后的△A3B3C.

参考答案:
【答案】(1)作图见解析;点A1的坐标为(4,﹣1);(2)作图见解析;(3)作图见解析.
【解析】试题分析:(1)根据网格结构找出点A、B、C向下平移5个单位的对应点A1、B1、C1的位置,然后顺次连接即可,再根据平面直角坐标系写出点A1的坐标;
(2)根据网格结构找出点A、B、C关于点y轴对称的对应点A2、B2、C2的位置,然后顺次连接即可,再根据平面直角坐标系写出点A2的坐标即可;
(3)根据三角形的面积公式求出△ABC的面积.
试题解析:(1)如图所示,△A1B1C1即为所求作的三角形,点A1的坐标(4,-1);
(2)如图所示,△A2B2C2即为所求作的三角形;A2(-4,-1);
(3)S△ABC=![]() ×2×2=2.
×2×2=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三角形
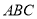 中,
中, ,
,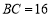 ,
,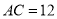 .点
.点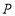 从点
从点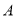 出发以2个单位长度/秒的速度沿
出发以2个单位长度/秒的速度沿 的方向运动,点
的方向运动,点 从点
从点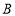 沿
沿 的方向与点
的方向与点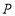 同时出发;当点
同时出发;当点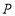 第一次回到
第一次回到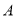 点时,点
点时,点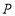 ,
, 同时停止运动;用
同时停止运动;用 (秒)表示运动时间.
(秒)表示运动时间.(1)当
 为多少时,
为多少时,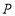 是
是 的中点;
的中点;(2)若点
 的运动速度是
的运动速度是 个单位长度/秒,是否存在
个单位长度/秒,是否存在 的值,使得
的值,使得 ;
;(3)若点
 的运动速度是
的运动速度是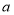 个单位长度/秒,当点
个单位长度/秒,当点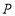 ,
, 是
是 边上的三等分点时,求
边上的三等分点时,求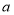 的值.
的值.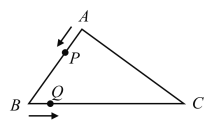
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(﹣3,4),B(﹣4,2),C(﹣2,1),△ABC绕原点逆时针旋转90°,得到△A1B1C1,将△A1B1C1向右平移6个单位,再向上平移2个单位得到△A2B2C2.
(1)画出△A1B1C1和△A2B2C2;
(2)△ABC经旋转、平移后点A的对应点分别为A1、A2,请写出点A1、A2的坐标;
(3)P(a,b)是△ABC的边AC上一点,△ABC经旋转、平移后点P的对应点分别为P1,P2,请写出点P1、P2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读并理解下面的证明过程,并在每步后的括号内填写该步推理的依据.如图,已知
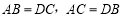 .求证:
.求证: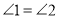 .
.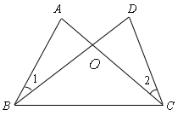
证明:在△ABC和△DCB中,
AB=DC(已知)
AC=DB(已知)
= ( )
∴△ABC≌△DCB( )
∴∠ABC=∠DCB,∠ACB=∠DBC( )
∴∠ABC-∠DBC=∠DCB-∠ACB即∠1=∠2
-
科目: 来源: 题型:
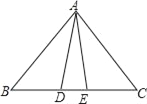
查看答案和解析>>【题目】如图,已知△ABE≌△ACD.
(1)如果BE=6,DE=2,求BC的长;
(2)如果∠BAC=75°,∠BAD=30°,求∠DAE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若
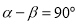 ,且
,且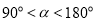 ,则我们称
,则我们称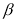 是
是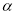 的差余角.例如:若
的差余角.例如:若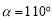 ,则
,则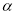 的差余角
的差余角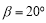 .
.(1)如图1,点
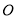 在直线
在直线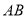 上,射线
上,射线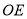 是
是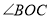 的角平分线,若
的角平分线,若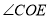 是
是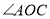 的差余角,求
的差余角,求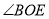 的度数.
的度数.(2)如图2,点
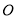 在直线
在直线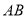 上,若
上,若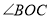 是
是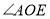 的差余角,那么
的差余角,那么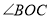 与
与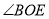 有什么数量关系.
有什么数量关系.(3)如图3,点
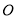 在直线
在直线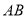 上,若
上,若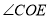 是
是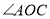 的差余角,且
的差余角,且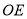 与
与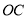 在直线
在直线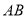 的同侧,请你探究
的同侧,请你探究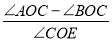 是否为定值?若是,请求出定值;若不是,请说明理由.
是否为定值?若是,请求出定值;若不是,请说明理由.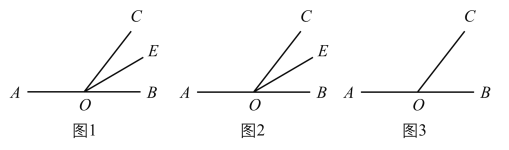
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列图形,它是把一个三角形分别连接其三边中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法,将这种做法继续下去(如图2,图3…).观察规律解答以下各题:
 ……
……(1)填写下表:
图形序号
挖去三角形的个数
图1
1
图2
1+3
图3
1+3+9
图4
(2)根据这个规律,求图n中挖去三角形的个数fn(用含n的代数式表示);
(3)若图n+1中挖去三角形的个数为fn+1,求fn+1-fn
相关试题

