【题目】如图,△ABC中,∠ACB=90°,∠ABC=60°,AB=8cm,D是AB的中点.现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M点.
(1)求证:AG=GH;
(2)求四边形GHME的面积.

参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】分析:(1)根据平移的性质可得△BCD≌△EFG,FG∥CD,EF∥CB,DG=EB=1,再根据直角三角形的性质可得AD=CD=BD=![]() AB=
AB=![]() ×8=4,然后再根据等边对等角,以及平行线的性质可得AG=GH;(2)过C作CN⊥AB于N,证明△BCD为等边三角形,利用勾股定理计算出CN,根据直角三角形的性质计算出MF,HM,再表示出△FHM和△FGE的面积,求差即可.
×8=4,然后再根据等边对等角,以及平行线的性质可得AG=GH;(2)过C作CN⊥AB于N,证明△BCD为等边三角形,利用勾股定理计算出CN,根据直角三角形的性质计算出MF,HM,再表示出△FHM和△FGE的面积,求差即可.
本题解析:
(1)证明:将△BCD沿BA方向平移得到△EFG,
∴△BCD≌△EFG,FG∥CD,EF∥CB,DG=EB=1,
∵∠ACB=90°,D是AB的中点,
∴AD=CD=BD=![]() AB=
AB=![]() ×8=4,
×8=4,
∴∠DAC=∠ACD,
∵FG∥CD,
∴∠AFG=∠ACD,
∴∠AHG=∠DAC,
∴AG=GH;
(2)解:如图:过C作CN⊥AB于N,
∵∠ABC=60°,∠ACB=90°,
∴∠A=30°,
∵BC=![]() AB=
AB=![]() ×8=4,
×8=4,
∵∠ABC=60°,CD=BD,
∴△BCD为等边三角形,
∴NB=![]() BD=2,
BD=2,
∴CN=![]() ,
,
∵DG=1,AD=4,
∴GH=AG=3,
∴FH=1,
∵∠A=30°,
∴∠A=30°=∠AHG=∠FHM=30°,
∵FE∥CB,∠ACB=90°,
∴MF=![]() ,
,
∴HM=![]() .
.
∴S△EFG=S△BCD=![]() ×4×2
×4×2![]() =4
=4![]() ,
,
S△MFH=![]() ×
×![]() ×
×![]() =
=![]() ,
,
∴S四边形GHME=4![]() ﹣
﹣![]() =
=![]() (cm2).
(cm2).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB交CD于O,OE⊥AB.
(1)若∠EOD=20°,求∠AOC的度数;
(2)若∠AOC:∠BOC=1:2,求∠EOD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是2015年12月月历.

(1)如图,用一正方形框在表中任意框住4个数,记左上角的一个数为x,则另三个数用含x的式子表示出来,从小到大依次是 , , .
(2)在表中框住四个数之和最小记为a1,和最大记为a2,则a1+a2= .
(3)当(1)中被框住的4个数之和等于76时,x的值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】红细胞的平均直径是0.0000072m,用科学记数法表示为m.
-
科目: 来源: 题型:
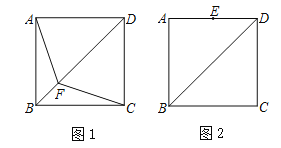
查看答案和解析>>【题目】已知:如图,正方形ABCD中,点F是对角线BD上的一个动点.
(1)如图1,连接AF,CF,直接写出AF与CF的数量关系;
(2)如图2,点E为AD边的中点,当点F运动到线段EC上时,连接AF,BE相交于点O.
①请你根据题意在图2中补全图形;
②猜想AF与BE的位置关系,并写出证明此猜想的思路;
③如果正方形的边长为2,直接写出AO的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程
 =
= x-3与方程3n
x-3与方程3n =3(x+n)-2n的解相同,求(2n-27)2的值.
=3(x+n)-2n的解相同,求(2n-27)2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(3a﹣2)﹣3(a﹣5)
(2)(4a2b﹣5ab2)﹣(3a2b﹣4ab2)
相关试题

