搜索
【题目】如图所示，在平面直角坐标系中，坐标原点O是菱形ABOC的一个顶点，边OB落在x轴的负半轴上，且cos∠BOC=
，顶点C的坐标为(a，4)，反比例函数
的图象与菱形对角线AO交于D点，连接BD，当BD⊥x轴时，k的值是（ ）
A. 
B. 
C. 
D. 
参考答案：
【答案】B
【解析】作CE⊥OB于点E;作AF⊥OB于点F.
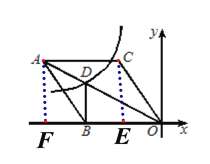
∵顶点C的坐标为(a，4)，
∴
.
∵cos∠BOC=
，
∴
，
∴a=-3或a=3（舍去）.
∴OE=3，OB=OC=5,AF=CE=4，
∴OF=OB+BF=OB+OE=5+3=8,
∴A(8,4).
设OA的解析式为:y=mx,
把A(-8,4)代入y=mx得，
-8m=4,
∴
,
∴
,
当x=-5时，
∴
，
∴
，
把
代入
得，
故选B.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠ACB＝90°，AC＝BC，直线MN经过点C，且AD⊥MN，BE⊥MN，垂足分别为点D，E．求证：DE＝AD＋BE．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y1=kx+b的图象与反比例函数
的图象交于点A（﹣2，﹣5），C（5，n），交y轴于点B，交x轴于点D．（1）求反比例函数
和一次函数y1=kx+b的表达式；（2）连接OA，OC，求△AOC的面积；
（3）根据图象，直接写出y1＞y2时x的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)经过点 经过点A（﹣1，0），B（5，﹣6），C（6，0）
（1）求抛物线的解析式；
（2）如图，在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大？若存在，请求出点P的坐标；若不存在，请说明理由；
（3）若点Q为抛物线的对称轴上的一个动点，试指出△QAB为等腰三角形的点Q一共有几个？并请求出其中某一个点Q的坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了解某县2011年初中毕业生的实验考查成绩等级的分布情况，随机抽取了该县若干名学生的实验考查成绩进行统计分析，并根据抽取的成绩绘制了如下的统计图表：
成绩等级
A
B
C
D
人数
60
x
y
10
百分比
30%
50%
15%
m
请根据以上统计图表提供的信息，解答下列问题：
⑴本次抽查的学生有___________________名；
⑵表中x，y和m所表示的数分别为：x=________，y=______，m=_________；
⑶请补全条形统计图；
⑷根据抽样调查结果，请你估计2011年该县5400名初中毕业生实验考查成绩为D类的学生人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图
，相邻两条平行直线间的距离相等，若等腰直角三角形ABC的直角顶点C在
上，另两个顶点A、B分别在
、
上，则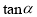
的值是_______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某大型企业为了保护环境，准备购买A、B两种型号的污水处理设备共8台，用于同时治理不同成分的污水，若购买A型2台、B型3台需54万，购买A型4台、B型2台需68万元．
（1）求出A型、B型污水处理设备的单价；
（2）经核实，一台A型设备一个月可处理污水220吨，一台B型设备一个月可处理污水190吨，如果该企业每月的污水处理量不低于1565吨，请你为该企业设计一种最省钱的购买方案．
相关试题
