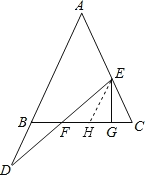
【题目】如图,在△ABC中,AB=AC,E在线段AC上,D在AB的延长线,连DE交BC于F,过点E作EG⊥BC于G.
(1)若∠A=50°,∠D=30°,求∠GEF的度数;
(2)若BD=CE,求证:FG=BF+CG.

参考答案:
【答案】(1)55°;(2)见解析
【解析】
(1)根据等腰三角形两底角相等及三角形内角和定理求出∠C,再根据直角三角形两锐角互余求出∠CEG,然后根据三角形的外角的性质求出∠CEF,即可得到结论;
(2)过点E作EH∥AB交BC于H,根据平行线的性质可得∠ABC=∠EHC,∠D=∠FEH,然后求出∠EHC=∠C,再根据等角对等边可得EC=EH,得出BD=EH,再利用“角角边”证明△BDF和△HEF全等,根据全等三角形对应边相等可得BF=FH,根据等腰三角形三线合一的性质可得CG=HG,即可得到结论.
(1)∵∠A=50°,∴∠C![]() (180°﹣∠A)
(180°﹣∠A)![]() (180°﹣50°)=65°.
(180°﹣50°)=65°.
∵EG⊥BC,∴∠CEG=90°﹣∠C=90°﹣65°=25°.
∵∠A=50°,∠D=30°,∴∠CEF=∠A+∠D=50°+30°=80°,∴∠GEF=∠CEF﹣∠CEG=80°﹣25°=55°;
(2)过点E作EH∥AB交BC于H,则∠ABC=∠EHC,∠D=∠FEH.
∵AB=AC,∴∠ABC=∠C,∴∠EHC=∠C,∴EC=EH.
∵BD=CE,∴BD=EH.
在△BDF和△HEF中,∵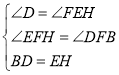 ,∴△BDF≌△HEF(AAS),∴BF=FH.
,∴△BDF≌△HEF(AAS),∴BF=FH.
又∵EC=EH,EG⊥BC,∴CG=HG,∴FG=FH+HG=BF+CG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】课本的作业题中有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形,你能办到吗?请画示意图说明剪法.
我们有多少种剪法,图1是其中的一种方法:

定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数;(若两种方法分得的三角形成3对全等三角形,则视为同一种)
(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=
 ,∠B=
,∠B= ,CD是AB边上的高;CE是∠ACB的平分线,DF⊥CE于F,求∠BCE和∠CDF的度数.
,CD是AB边上的高;CE是∠ACB的平分线,DF⊥CE于F,求∠BCE和∠CDF的度数.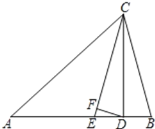
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE.试说明下列结论正确的理由:

(1)△ABC≌△ADE;
(2)AD平分∠BDE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某书店参加某校读书活动,并为每班准备了A,B两套名著,赠予各班甲、乙两名优秀读者,以资鼓励.某班决定采用游戏方式发放,其规则如下:将三张除了数字2,5,6不同外其余均相同的扑克牌,数字朝下随机平铺于桌面,从中任取2张,若牌面数字之和为偶数,则甲获A名著;若牌面数字之和为奇数,则乙获得A名著,你认为此规则合理吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC是边长为3的等边三角形,以BC为底边作一个顶角为120
 等腰△BDC.点M、点N分别是AB边与AC边上的点,并且满足∠MDN=60
等腰△BDC.点M、点N分别是AB边与AC边上的点,并且满足∠MDN=60
(1)如图1,当点D在△ABC外部时,求证:BM+CN=MN;
(2)当点D在△ABC内部时,其它条件不变,请在图2中补全图形,并直接写出△AMN的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是


A.
 B.
B. C.
C. D.
D.
相关试题

