搜索
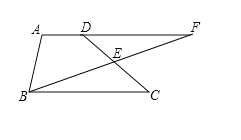
【题目】已知：如图，梯形ABCD中，AD∥BC，点E是CD的中点，BE的延长线与AD的延长线相交于点F．
（1）求证：△BCE≌△FDE．
（2）连接BD，CF，判断四边形BCFD的形状，并证明你的结论．
参考答案：
【答案】（1）见解析；（2）四边形BCFD是平行四边形，理由见解析
【解析】
（1）由平行线的性质可证，∠DFE=∠EBC，∠FDE=∠ECB，又已知DE=CE，在△BCE与△FDE中，根据三角形全等的判定定理，符合AAS的条件，即证△BCE≌△FDE．
（2）在1的基础上，可证DE=CE，FE=BE，根据平行四边形的判定，即证四边形BCFD是平行四边形．
证明：（1）∵点E是DC中点∴DE=CE
又∵AD∥BC，F在AD延长线上，∴∠DFE=∠EBC，∠FDE=∠ECB
在△BCE与△FDE中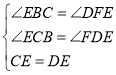
．
∴△BCE≌△FDE（AAS）
（2）四边形BCFD是平行四边形．理由如下：
∵△BCE≌△FDE，
∴DE=CE，FE=BE．
∴四边形BCFD是平行四边形．．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在Rt△ABC中，∠A=90°，AB=6，AC=8，点D为边BC的中点，DE⊥BC交边AC于点E，点P为射线AB上一动点，点Q为边AC上一动点，且∠PDQ=90°．
（1）求ED、EC的长；
（2）若BP=2，求CQ的长；
（3）记线段PQ与线段DE的交点为点F，若△PDF为等腰三角形，求BP的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商场销售国外、国内两种品牌的智能手机，这两种手机的进价和售价如表所示
国外品牌
国内品牌
进价（万元/部）
0.44
0.2
售价（万元/部）
0.5
0.25
该商场计划购进两种手机若干部，共需14.8万元，预计全部销售后可获毛利润共2.7万元．[毛利润=（售价﹣进价）×销售量]
（1）该商场计划购进国外品牌、国内品牌两种手机各多少部？
（2）通过市场调研，该商场决定在原计划的基础上，减少国外品牌手机的购进数量，增加国内品牌手机的购进数量．已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍，而且用于购进这两种手机的总资金不超过15.6万元，该商场应该怎样进货，使全部销售后获得的毛利润最大？并求出最大毛利润
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，AC为对角线，E为AB上一点，过点E作EF∥AD，与AC、DC分别交于点G，F，H为CG的中点，连接DE，EH，DH，FH．下列结论：
①EG=DF；②∠AEH+∠ADH=180 ；③△EHF≌△DHC；④若
，则3S△EDH=13S△DHC，其中结论正确的有___________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y＝ax2＋bx＋c经过A(－1，0)、B(3，0)、C(0，3)三点，直线l是抛物线的对称轴．
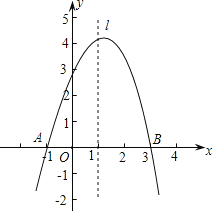
(1)求抛物线的函数关系式；
(2)设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；
(3)在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A、B、C在一条直线上，
，
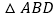均为等边三角形，连接AE、CD.AE分别交CD、BD于点M．P.CD交BE于点Q．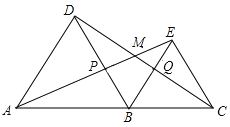
求证：（1）
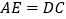；（2）连接MB，MB平分
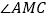吗？并说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知数轴上三点A、O、B对应的数分别为﹣3，0，1，点P为数轴上任意一点，其表示的数为x．
（1）如果点P到点A，点B的距离相等，那么x＝ ；
（2）当x＝ 时，点P到点A、点B的距离之和是6；
（3）若点P到点A，点B的距离之和最小，则x的取值范围是 ；
（4）若点P到点A，点B，点O的距离之和最小，则最小距离为 ．
相关试题
