【题目】如图,点A、B、C在一条直线上,![]() ,
,![]() 均为等边三角形,连接AE、CD.AE分别交CD、BD于点M.P.CD交BE于点Q.
均为等边三角形,连接AE、CD.AE分别交CD、BD于点M.P.CD交BE于点Q.
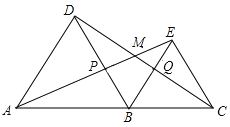
求证:(1)![]() ;
;
(2)连接MB,MB平分![]() 吗?并说明理由.
吗?并说明理由.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据等边三角形的选择证明得出:△ABE≌ODBC即可
(2)连接MB,根据垂直定理即可证明∠l=∠2,再根据全等三角形的性质可得BI= BJ.即可证明MB平分LAMC.
(1) ![]() △ABD, △BCE均为等边三角形,
△ABD, △BCE均为等边三角形,
![]() AB= DB,EB=CB,∠ABD=∠C BE= 60°
AB= DB,EB=CB,∠ABD=∠C BE= 60°
![]() ∠ABD+∠DBE=∠CBE+∠DBE即∠ABE=∠DBC
∠ABD+∠DBE=∠CBE+∠DBE即∠ABE=∠DBC
![]() △ABE≌ODBC
△ABE≌ODBC
![]() AE= DC.
AE= DC.
(2)

连接MB,MB平分∠AMC,
理由是:作BI⊥AE于点I, BJ⊥DC于点J,则∠AIB=∠DJB=90°.
由(1)知,△ABE≌ODBC,AB= DB
![]() ∠l=∠2,
∠l=∠2,
△ABI≌△DBJ
![]() BI= BJ.
BI= BJ.
MB平分∠AMC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论:
①EG=DF;②∠AEH+∠ADH=180 ;③△EHF≌△DHC;④若
 ,则3S△EDH=13S△DHC,其中结论正确的有___________.
,则3S△EDH=13S△DHC,其中结论正确的有___________.
-
科目: 来源: 题型:
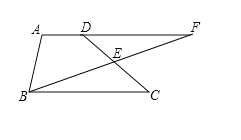
查看答案和解析>>【题目】已知:如图,梯形ABCD中,AD∥BC,点E是CD的中点,BE的延长线与AD的延长线相交于点F.
(1)求证:△BCE≌△FDE.
(2)连接BD,CF,判断四边形BCFD的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
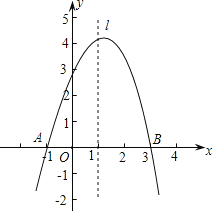
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点A、O、B对应的数分别为﹣3,0,1,点P为数轴上任意一点,其表示的数为x.
(1)如果点P到点A,点B的距离相等,那么x= ;
(2)当x= 时,点P到点A、点B的距离之和是6;
(3)若点P到点A,点B的距离之和最小,则x的取值范围是 ;
(4)若点P到点A,点B,点O的距离之和最小,则最小距离为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解家长关注孩子成长方面的状况,学校开展了针对学生家长的“您最关心孩子哪方面成长”的主题调查,调查设置了“健康安全”、“日常学习”、“习惯养成”、“情感品质”四个项目,并随机抽取甲、乙两班共100位学生家长进行调查,根据调查结果,绘制了如图不完整的条形统计图.
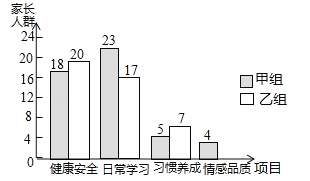
(1)补全条形统计图.
(2)若全校共有3600位学生家长,据此估计,有多少位家长最关心孩子“情感品质”方面的成长?
(3)综合以上主题调查结果,结合自身现状,你更希望得到以上四个项目中哪方面的关注和指导?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某种特制的计算器中有一个按键
 ,它代表运算
,它代表运算 .
. 例如:
例如:
上述操作即是求
 的值,运算结果为1.
的值,运算结果为1.回答下面的问题:
(1)小敏的输入顺序为﹣6,
 ,﹣8,
,﹣8, ,运算结果是 ;
,运算结果是 ;(2)小杰的输入顺序为1,
 ,-
,-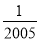 ,
, ,
, ,﹣2,
,﹣2, ,-
,- ,
, ,
, ,3,
,3, ,运算结果是 ;
,运算结果是 ;(3)若在
 这些数中,任意选取两个作为a、b的值,进行
这些数中,任意选取两个作为a、b的值,进行 运算,则所有的运算结果中最大的值是 .
运算,则所有的运算结果中最大的值是 .
相关试题

