Question

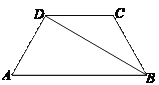
【题目】如图，在等腰梯形ABCD中，DC∥AB，AD＝BC=2，BD平分∠ABC．∠A＝60°，求对角线BD的长和梯形ABCD的面积．

Answer 1

【答案】2,3

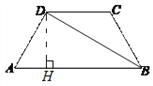
【解析】分析：过点D作DH⊥AB，垂足为H.利用等腰梯形的性质证△ABD与△DBH均为含30度角的直角三角形，即可求出AB、BD、DH的长，再利用平行及角平分线证明△BCD为等腰三角形即可得出DC的长，最后利用梯形的面积公式求解即可.

详解：过点D作DH⊥AB，垂足为H.

在等腰梯形ABCD中，

∵∠A=60°，

∴∠ABC=∠A=60°，

∵BD平分∠ABC，

∴∠ABD=∠CBD =30°，

在△ABD中，

∵∠A+∠ABD+∠ADB=180°，

∴∠ADB=90°

∴AD=AB，

∵AD=2，

∴AB=4．

∴由勾股定理BD=，

在Rt△BDH中，

∵∠DBH=30°，

∴DH=BD=，

∵DC∥AB，

∴∠ABD=∠CDB，

又∵∠ABD=∠CBD，

∴∠CDB=∠CBD，

∴CD=BC=2，

∴．