【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC= ![]() ,反比例函数y=
,反比例函数y= ![]() 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于 .
的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于 . 
参考答案:
【答案】﹣24
【解析】解:作DE∥AO,CF⊥AO,设CF=4x, 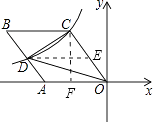
∵四边形OABC为菱形,
∴AB∥CO,AO∥BC,
∵DE∥AO,
∴S△ADO=S△DEO ,
同理S△BCD=S△CDE ,
∵S菱形ABCO=S△ADO+S△DEO+S△BCD+S△CDE ,
∴S菱形ABCO=2(S△DEO+S△CDE)=2S△CDO=40,
∵tan∠AOC= ![]() ,
,
∴OF=3x,
∴OC= ![]() =5x,
=5x,
∴OA=OC=5x,
∵S菱形ABCO=AOCF=20x2 , 解得:x= ![]() ,
,
∴OF= ![]() ,CF=
,CF= ![]() ,
,
∴点C坐标为(﹣ ![]() ,
, ![]() ),
),
∵反比例函数y= ![]() 的图象经过点C,
的图象经过点C,
∴代入点C得:k=﹣24,
所以答案是﹣24.
【考点精析】解答此题的关键在于理解比例系数k的几何意义的相关知识,掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积,以及对菱形的性质的理解,了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,描述了林老师某日傍晚的一段生活过程:他晚饭后,从家里散步走到超市,在超市停留了一会儿,马上又去书店,看了一会儿书,然后快步走回家,图象中的平面直角坐标系中x表示时间,y表示林老师离家的距离,请你认真研读这个图象,根据图象提供的信息,以下说法错误的是( )

A. 林老师家距超市1.5千米
B. 林老师在书店停留了30分钟
C. 林老师从家里到超市的平均速度与从超市到书店的平均速度是相等的
D. 林老师从书店到家的平均速度是10千米/时
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC经过平移之后成为△DEF,那么:
(1)点A的对应点是点________;
(2)点________的对应点是点F;
(3)线段AB的对应线段是线段________;
(4)线段BC的对应线段是线段________;
(5)∠A的对应角是________;
(6)________的对应角是∠F.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区准备在甲乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同.
第1次
第2次
第3次
第4次
第5次
甲成绩
9
4
7
4
6
乙成绩
7
5
7
a
7
(1)a=__,
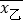 =____;
=____;(2)①分别计算甲、乙成绩的方差.
②请你从平均数和方差的角度分析,谁将被选中.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在扇形AOB中,∠AOB=90°,以点A为圆心,OA的长为半径作
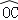 交
交 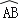 于点C,若OA=2,则阴影部分的面积为 .
于点C,若OA=2,则阴影部分的面积为 . 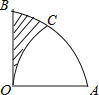
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=ax+b的图像与正比例函数y=kx的图像交于点M,
(1)求正比例函数和一次函数的解析式;
(2)根据图像写出使正比例函数的值大于一次函数的值的x的取值范围;
(3)求ΔMOP的面积。

-
科目: 来源: 题型:
查看答案和解析>>【题目】花园内有一块边长为a的正方形土地,园艺师设计了三种不同的图案,如图①②③所示,其中的阴影部分用于种植花草,试比较三种方案中用于种植花草部分的面积的大小,并用平移的知识说明理由.

相关试题

