【题目】如图,一次函数y=kx+3分别与x,y轴交于点N,M,与反比例函数y= ![]() (x>0)的图象交于点A,若AM:MN=2:3,则k= .
(x>0)的图象交于点A,若AM:MN=2:3,则k= . 
参考答案:
【答案】![]()
【解析】解:过点A作AB⊥x轴于点B,如图所示.

∵AB⊥x轴,MO⊥x轴,
∴AB∥MO,
∴△NMO∽△NAB,
∴ ![]() .
.
∵AM:MN=2:3,
MN:AN=3:(2+3)=3:5.
令一次函数y=kx+3中x=0,则y=3,
∴MO=3.
∵ ![]() =
= ![]() ,
,
∴AB=5,
令反比例函数y= ![]() 中y=5,则5=
中y=5,则5= ![]() ,
,
解得:x= ![]() .
.
∴点A的坐标为( ![]() ,5).
,5).
将点A( ![]() ,5)代入一次函数y=kx+3中,
,5)代入一次函数y=kx+3中,
得:5= ![]() k+3,解得:k=
k+3,解得:k= ![]() .
.
所以答案是: ![]() .
.
【考点精析】通过灵活运用相似三角形的判定与性质,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,在△ABC中,AB=AC,分别以AB、BC为边作等边△ABE和等边△BCD,连结CE、AD.
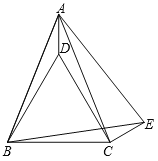
(1)求证:∠ACD=∠ABD;
(2)判断DC与CE的位置关系,并加以证明;
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中,对角线AC与BD交于点O,下列各组条件,其中不能判定四边形ABCD是平行四边形的是( )
A. OA=OC,OB=ODB. OA=OC,AB∥CD
C. AB=CD,OA=OCD. ∠ADB=∠CBD,∠BAD=∠BCD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,点
,点 在
在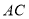 上,以
上,以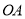 为半径的
为半径的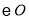 交
交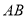 于点
于点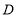 ,
,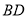 的垂直平分线交
的垂直平分线交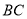 于点
于点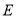 ,交
,交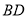 于点
于点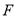 ,连接
,连接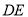 .
.(1)判断直线
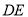 与
与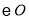 的位置关系,并说明理由;
的位置关系,并说明理由;(2)若
 ,
,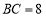 ,
,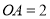 ,求线段
,求线段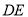 的长.
的长.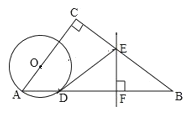
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CN是等边△ABC的外角∠ACM内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
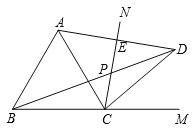
(1)求证:CD=CB;
(2)若∠ACN= a,求∠BDC的大小(用含a的式子表示);
(3)请判断线段PB,PC与PE三者之间的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论:
①AM=AD+MC;②AM=DE+BM;③DE2=ADCM;④点N为△ABM的外心.其中正确的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示的正整数后,背面向上,洗匀放好.

(1)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,嘉嘉从中随机抽取一张,求抽到的卡片上的数是勾股数的概率P1;
(2)琪琪从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张(卡片用A,B,C,D表示).请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2 , 并指出她与嘉嘉抽到勾股数的可能性一样吗?
相关试题

