【题目】对于平面直角坐标系![]() 中的图形M和点P(点P在M内部或M上),给出如下定义:
中的图形M和点P(点P在M内部或M上),给出如下定义:
如果图形M上存在点Q,使得![]() ,那么称点P为图形M的和谐点.
,那么称点P为图形M的和谐点.
已知点![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)在点![]() ,
,![]() ,
,![]() 中,矩形
中,矩形![]() 的和谐点是_________________;
的和谐点是_________________;
(2)如果直线![]() 上存在矩形
上存在矩形![]() 的和谐点P,求出点P的横坐标t的取值范围;
的和谐点P,求出点P的横坐标t的取值范围;
(3)如果直线![]() 上存在矩形
上存在矩形![]() 的和谐点E,F,使得线段
的和谐点E,F,使得线段![]() 上的所有点(含端点)都是矩形
上的所有点(含端点)都是矩形![]() 的和谐点,且
的和谐点,且![]() ,求出b的取值范围.
,求出b的取值范围.
参考答案:
【答案】(1)![]() 和
和![]() ;(2)
;(2) ![]() 或
或![]() ;(3) 2≤b<3或-3<b≤-2.
;(3) 2≤b<3或-3<b≤-2.
【解析】
(1)如下图1中,根据点P为图形M的和谐点的定义,观察图形可知P1和P3是矩形ABCD的和谐点.
(2)如图2中,求出满足条件的P1、P2、P3、P4的坐标即可判断.
(3)当b=3时,图中线段EF上的点都是和谐点,且![]() ,当将直线往y轴负半轴平移时刚好经过点M,此时
,当将直线往y轴负半轴平移时刚好经过点M,此时![]() 上的点都是和谐点,且
上的点都是和谐点,且![]() ,当再往下平移时,EF上有部分点不再是和谐点,由此求出b的范围为2≤b<3;根据对称性,-3<b≤-2也满足.
,当再往下平移时,EF上有部分点不再是和谐点,由此求出b的范围为2≤b<3;根据对称性,-3<b≤-2也满足.
(1)如下图1中,根据点P为图形M的和谐点的定义,观察图形可知:

![]() 到矩形边AD和AB的最短距离为2,符合和谐点的定义;
到矩形边AD和AB的最短距离为2,符合和谐点的定义;
![]() 到矩形四边的距离均大于2,不符合和谐点的定义;
到矩形四边的距离均大于2,不符合和谐点的定义;
![]() 是矩形边AD的距离为0,符合和谐点的定义;
是矩形边AD的距离为0,符合和谐点的定义;
故是和谐点的是点![]() 和
和![]() .
.
故答案为:![]() 和
和![]() .
.
(2)如图2中:

当直线![]() 上的点P到直线AB的距离为2时,可得
上的点P到直线AB的距离为2时,可得![]() 和
和![]() 均满足和谐点的定义,此时
均满足和谐点的定义,此时![]() 均是和谐点,故此时
均是和谐点,故此时![]() 的取值范围是:
的取值范围是:![]() ;
;
当直线![]() 上的点P到直线AD的距离为2时,可得
上的点P到直线AD的距离为2时,可得![]() 和
和![]() 均满足和谐点的定义,此时
均满足和谐点的定义,此时![]() 均是和谐点,故此时
均是和谐点,故此时![]() 的取值范围是:
的取值范围是:![]() ;
;
故满足条件的![]() 的取值范围是:
的取值范围是:![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.
(3)如下图3所示:

当b=3时,图中线段EF上的点都是和谐点,且![]() ,
,
当将直线往y轴负半轴平移且刚好经过点M(-2,1),
将点M(-2,1)代入解析式![]() ,
,
即:![]() ,解得:b=2,且此时
,解得:b=2,且此时![]()
故此时b的范围为2≤b<3,
同理,由对称性可知,当-3<b≤-2也满足条件.
故b的取值范围为:2≤b<3或-3<b≤-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=30°,以AB为直径的⊙O经过点C.过点C作⊙O的切线交AB的延长线于点P.点D为圆上一点,且
 ,弦AD的延长线交切线PC于点E,连接BC.
,弦AD的延长线交切线PC于点E,连接BC.(1)判断OB和BP的数量关系,并说明理由;
(2)若⊙O的半径为2,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】暴雨过后,某地遭遇山体滑坡,武警总队派出一队武警战士前往抢险. 半小时后,第二队前去支援,平均速度是第一队的1.5倍,结果两队同时到达.已知抢险队的出发地与灾区的距离为90千米,两队所行路线相同,问两队的平均速度分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,部分同学随家长一同到某公园游玩,下面是购买门票时,甲同学与其爸爸的对话(如图),试根据图中的信息,解决下列问题:
票 价
成人:每人80元
学生:按成人票价五折优惠
团体票:16人以上(含16人),每人按成人票价六折优惠
 成人门票每张80元,学生门票五折优惠,我们一共12人,共需800元.
成人门票每张80元,学生门票五折优惠,我们一共12人,共需800元. 爸爸,等一下,让我算一算,换一种方式,购票是否可以省钱.
爸爸,等一下,让我算一算,换一种方式,购票是否可以省钱.(1)本次共去了几个成人,几个学生?
(2)甲同学所说的另一种购票方式,是否可以省钱?试说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
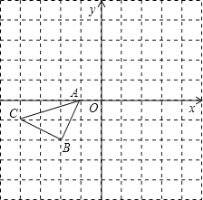
(1)作出△ABC绕点A逆时针旋转90°的△AB1C1.
(2)作出△AB1C1关于原点O成中心对称的△A1B2C2.
(3)请直接写出以A1、B2、C2为顶点的平行四边形的第四个顶点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 ,
, 与
与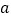 ,
, 分别相交于点
分别相交于点 ,
, ,且
,且 ,
, 交直线
交直线 于点
于点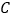 .
.
(1)若
 ,求
,求 的度数;
的度数;(2)若
 ,
,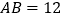 ,
, ,求直线
,求直线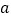 与
与 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】网瘾低龄化问题已引起社会各界的高度关注,有关部门在全国范围内对
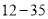 岁的网瘾人群进行了简单的随机抽样调查,得到了如图所示的两个不完全统计图.
岁的网瘾人群进行了简单的随机抽样调查,得到了如图所示的两个不完全统计图.请根据图中的信息,解决下列问题:
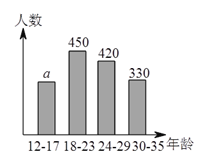
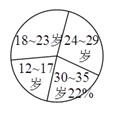
(
 )求条形统计图中
)求条形统计图中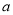 的值.
的值.(
 )求扇形统计图中
)求扇形统计图中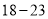 岁部分所占的百分比;
岁部分所占的百分比;(
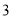 )据报道,目前我国
)据报道,目前我国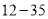 岁网瘾人数约为
岁网瘾人数约为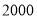 万,请估计其中
万,请估计其中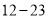 岁的人数.
岁的人数.
相关试题

