【题目】小明合作学习小组在探究旋转、平移变换.如图△ABC,DEF均为等腰直角三角形,各顶点坐标分别为A(1,1),B(2,2),C(2,1),D( ![]() ,0),E(2
,0),E(2 ![]() ,0),F(
,0),F( ![]() ,﹣
,﹣ ![]() ).
).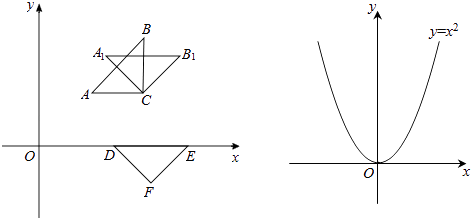
(1)他们将△ABC绕C点按顺时针方向旋转45°得到△A1B1C1 . 请你写出点A1 , B1的坐标,并判断A1C和DF的位置关系;
(2)他们将△ABC绕原点按顺时针方向旋转45°,发现旋转后的三角形恰好有两个顶点落在抛物线y=2 ![]() x2+bx+c上,请你求出符合条件的抛物线解析式;
x2+bx+c上,请你求出符合条件的抛物线解析式;
(3)他们继续探究,发现将△ABC绕某个点旋转45°,若旋转后的三角形恰好有两个顶点落在抛物线y=x2上,则可求出旋转后三角形的直角顶点P的坐标,请你直接写出点P的所有坐标.
参考答案:
【答案】
(1)
解:A1(2﹣ ![]() ,1+
,1+ ![]() ),B1(2+
),B1(2+ ![]() ,1+
,1+ ![]() ).
).
A1C和DF的位置关系是平行
(2)
解:∵△ABC绕原点按顺时针方向旋转45°后的三角形即为△DEF,
∴①当抛物线经过点D、E时,根据题意可得:
![]() ,
,
解得 ![]()
∴y= ![]() x2﹣12x+
x2﹣12x+ ![]() ;
;
②当抛物线经过点D、F时,根据题意可得:
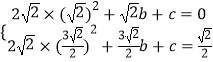 ,
,
解得 ![]()
∴y= ![]() x2﹣11x+
x2﹣11x+ ![]() ;
;
③当抛物线经过点E、F时,根据题意可得:
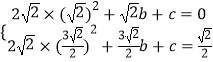 ,
,
解得 ![]()
∴y= ![]() x2﹣13x+
x2﹣13x+ ![]()
(3)
解:在旋转过程中,可能有以下情形:
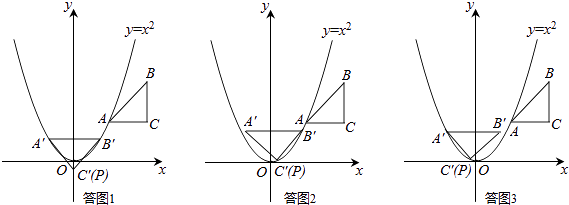
①顺时针旋转45°,点A、B落在抛物线上,如答图1所示:
易求得点P坐标为(0, ![]() );
);
②顺时针旋转45°,点B、C落在抛物线上,如答图2所示:
设点B′,C′的横坐标分别为x1,x2.
易知此时B′C′与一、三象限角平分线平行,∴设直线B′C′的解析式为y=x+b,
联立y=x2与y=x+b得:x2=x+b,即x2﹣x﹣b=0,
∴x1+x2=1,x1x2=﹣b.
∵B′C′=1,∴根据题意易得:|x1﹣x2|= ![]() ,
,
∴(x1﹣x2)2= ![]() ,即(x1+x2)2﹣4x1x2=
,即(x1+x2)2﹣4x1x2= ![]()
∴1+4b= ![]() ,解得b=-
,解得b=- ![]() .
.
∴x2﹣x+ ![]() =0,解得x=
=0,解得x= ![]() 或x=
或x= ![]() .
.
∵点C′的横坐标较小,∴x= ![]() .
.
当x= ![]() 时,y=x2=
时,y=x2= ![]() ,
,
∴P( ![]() ,
, ![]() );
);
③顺时针旋转45°,点C、A落在抛物线上,如答图3所示:
设点C′,A′的横坐标分别为x1,x2.
易知此时C′A′与二、四象限角平分线平行,∴设直线C′A′的解析式为y=﹣x+b,
联立y=x2与y=﹣x+b得:x2=﹣x+b,即x2+x﹣b=0,
∴x1+x2=﹣1,x1x2=﹣b.
∵C′A′=1,∴根据题意易得:|x1﹣x2|= ![]() ,
,
∴(x1﹣x2)2= ![]() ,即(x1+x2)2﹣4x1x2=
,即(x1+x2)2﹣4x1x2= ![]()
∴1+4b= ![]() ,解得b=-
,解得b=- ![]() .
.
∴x2+x+ ![]() =0,解得x=
=0,解得x= ![]() 或x=
或x= ![]() .
.
∵点C′的横坐标较大,∴x= ![]() .
.
当x= ![]() 时,y=x2=
时,y=x2= ![]() ,
,
∴P( ![]() ,
, ![]() );
);
④逆时针旋转45°,点A、B落在抛物线上.
因为逆时针旋转45°后,直线A′B′与y轴平行,因此,与抛物线最多只能有一个交点,故此种情形不存在;
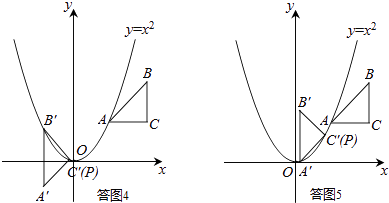
⑤逆时针旋转45°,点B、C落在抛物线上,如答图4所示:
与③同理,可求得:P( ![]() ,
, ![]() );
);
⑥逆时针旋转45°,点C、A落在抛物线上,如答图5所示:
与②同理,可求得:P( ![]() ,
, ![]() ).
).
综上所述,点P的坐标为:(0, ![]() ),(
),( ![]() ,
, ![]() ),(
),( ![]() ,
, ![]() ),(
),( ![]() ,
, ![]() )
)
【解析】(1)由旋转性质及等腰直角三角形边角关系求解;(2)首先明确△ABC绕原点按顺时针方向旋转45°后的三角形即为△DEF,然后分三种情况进行讨论,分别计算求解;(3)旋转方向有顺时针、逆时针两种可能,落在抛物线上的点有点A和点B、点B和点C、点C和点D三种可能,因此共有六种可能的情形,需要分类讨论,避免漏解.
【考点精析】本题主要考查了平移的性质和旋转的性质的相关知识点,需要掌握①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.
采购数量(件)
1
2
…
A产品单价(元/件)
1480
1460
…
B产品单价(元/件)
1290
1280
…
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的 ,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读,后解答:
(1)由根式的性质计算下列式子得:
①
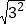 =3,②
=3,②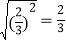 ,③
,③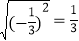 ,④
,④ =5,⑤
=5,⑤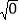 =0.
=0.由上述计算,请写出
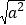 的结果(a为任意实数).
的结果(a为任意实数).(2)利用(1)中的结论,计算下列问题的结果:
①
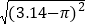 ;
;②化简:
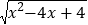 (x<2).
(x<2).(3)应用:
若
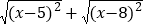 =3,求x的取值范围.
=3,求x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC三边长a=b=6
 ,c=12.
,c=12.(1)如图1,以点A为原点,AB所在直线为x轴建立平面直角坐标系,直接出点B,C的坐标.
(2)如图2,过点C作∠MCN=45°交AB于点M,N,请证明AM2+BN2=MN2;
(3)如图3,当点M,N分布在点B异侧时,则(3)中的结论还成立吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示):使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50cm,第2节套管长46cm,以此类推,每一节套管均比前一节套管少4cm.完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为xcm.

(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为311cm,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,已知y=
 (x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0),动点M是y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q连接AQ,取AQ的中点为C.
(x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0),动点M是y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q连接AQ,取AQ的中点为C.
(1)如图2,连接BP,求△PAB的面积;
(2)当点Q在线段BD上时,若四边形BQNC是菱形,面积为2 ,求此时P点的坐标;
,求此时P点的坐标;
(3)当点Q在射线BD上时,且a=3,b=1,若以点B,C,N,Q为顶点的四边形是平行四边形,求这个平行四边形的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y1=ax2﹣4ax+3(a≠0)与y轴交于点A,A、B两点关于对称轴对称,直线OB分别与抛物线的对称轴相交于点C.
(1)直接写出对称轴及B点的坐标;
(2)已知直线y2=bx﹣4b+3(b≠0)与抛物线的对称轴相交于点D. ①判断直线y2=bx﹣4b+3(b≠0)是否经过点B,并说明理由;
②若△BDC的面积为1,求b的值.
相关试题

