【题目】如图1所示,已知y= ![]() (x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0),动点M是y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q连接AQ,取AQ的中点为C.
(x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0),动点M是y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q连接AQ,取AQ的中点为C.
(1)如图2,连接BP,求△PAB的面积;
(2)当点Q在线段BD上时,若四边形BQNC是菱形,面积为2 ![]() ,求此时P点的坐标;
,求此时P点的坐标;
(3)当点Q在射线BD上时,且a=3,b=1,若以点B,C,N,Q为顶点的四边形是平行四边形,求这个平行四边形的周长.
参考答案:
【答案】
(1)
解:如图2,连接OP.
S△PAB=S△PAO= ![]() xy=
xy= ![]() ×6=3
×6=3

(2)
解:如图3,

∵四边形BQNC是菱形,
∴BQ=BC=NQ,∠BQC=∠NQC,
∵AB⊥BQ,C是AQ的中点,
∴BC=CQ= ![]() AQ,
AQ,
∴∠BQC=60°,∠BAQ=30°,
在△ABQ和△ANQ中,
 ,
,
∴△ABQ≌△ANQ(SAS),
∴∠BAQ=∠NAQ=30°,
∴∠BAO=30°,
∵S菱形BQNC=2 ![]() =
= ![]() ×CQ×BN,
×CQ×BN,
令CQ=2t=BQ,则BN=2×(2t× ![]() )=2
)=2 ![]() t,
t,
∴t=1
∴BQ=2,
∵在Rt△AQB中,∠BAQ=30°,
∴AB= ![]() BQ=2
BQ=2 ![]() ,
,
∵∠BAO=30°
∴OA= ![]() AB=3,
AB=3,
又∵P点在反比例函数y= ![]() 的图象上,
的图象上,
∴P点坐标为(3,2)
(3)
解:∵OB=1,OA=3,
∴AB= ![]() ,
,
易得△AOB∽△DBA,
∴ ![]() ,
,
∴BD=3 ![]() ,
,
①如图3,当点Q在线段BD上,

∵AB⊥BD,C为AQ的中点,
∴BC= ![]() AQ,
AQ,
∵四边形BQNC是平行四边形,
∴QN=BC,CN=BQ,CN∥BD,
∴ ![]() =
= ![]() ,
,
∴BQ=CN= ![]() BD=
BD= ![]() ,
,
∴AQ= ![]() =2
=2 ![]() ,
,
∴C四边形BQNC=2 ![]() +2
+2 ![]() ;
;
②如图4,当点Q在射线BD的延长线上,

∵AB⊥BD,C为AQ的中点,
∴BC=CQ= ![]() AQ,
AQ,
∴平行四边形BNQC是菱形,BN=CQ,BN∥CQ,
∴△BND∽△QAD
∴ ![]() =
= ![]() ,
,
∴BQ=3BD=9 ![]() ,
,
∴AQ= ![]() =
= ![]() =2
=2 ![]() ,
,
∴C四边形BNQC=2AQ=4 ![]() .
.
【解析】(1)根据同底等高的两个三角形的面积相等即可求出△PAB的面积;(2)首先求出∠BQC=60°,∠BAQ=30°,然后证明△ABQ≌△ANQ,进而求出∠BAO=30°,由S四边形BQNC=2 ![]() ,求出OA=3,于是P点坐标求出;(3)分两类进行讨论,当点Q在线段BD上,根据题干条件求出AQ的长,进而求出四边形的周长,当点Q在线段BD的延长线上,依然根据题干条件求出AQ的长,再进一步求出四边形的周长.
,求出OA=3,于是P点坐标求出;(3)分两类进行讨论,当点Q在线段BD上,根据题干条件求出AQ的长,进而求出四边形的周长,当点Q在线段BD的延长线上,依然根据题干条件求出AQ的长,再进一步求出四边形的周长.
【考点精析】本题主要考查了反比例函数的图象和反比例函数的性质的相关知识点,需要掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC三边长a=b=6
 ,c=12.
,c=12.(1)如图1,以点A为原点,AB所在直线为x轴建立平面直角坐标系,直接出点B,C的坐标.
(2)如图2,过点C作∠MCN=45°交AB于点M,N,请证明AM2+BN2=MN2;
(3)如图3,当点M,N分布在点B异侧时,则(3)中的结论还成立吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明合作学习小组在探究旋转、平移变换.如图△ABC,DEF均为等腰直角三角形,各顶点坐标分别为A(1,1),B(2,2),C(2,1),D(
 ,0),E(2
,0),E(2  ,0),F(
,0),F( 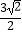 ,﹣
,﹣ 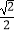 ).
).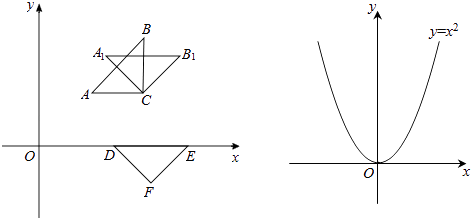
(1)他们将△ABC绕C点按顺时针方向旋转45°得到△A1B1C1 . 请你写出点A1 , B1的坐标,并判断A1C和DF的位置关系;
(2)他们将△ABC绕原点按顺时针方向旋转45°,发现旋转后的三角形恰好有两个顶点落在抛物线y=2 x2+bx+c上,请你求出符合条件的抛物线解析式;
x2+bx+c上,请你求出符合条件的抛物线解析式;
(3)他们继续探究,发现将△ABC绕某个点旋转45°,若旋转后的三角形恰好有两个顶点落在抛物线y=x2上,则可求出旋转后三角形的直角顶点P的坐标,请你直接写出点P的所有坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示):使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50cm,第2节套管长46cm,以此类推,每一节套管均比前一节套管少4cm.完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为xcm.

(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为311cm,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y1=ax2﹣4ax+3(a≠0)与y轴交于点A,A、B两点关于对称轴对称,直线OB分别与抛物线的对称轴相交于点C.
(1)直接写出对称轴及B点的坐标;
(2)已知直线y2=bx﹣4b+3(b≠0)与抛物线的对称轴相交于点D. ①判断直线y2=bx﹣4b+3(b≠0)是否经过点B,并说明理由;
②若△BDC的面积为1,求b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别为(﹣2,0),(﹣1,0),BC⊥x轴,将△ABC以y轴为对称轴作轴对称变换,得到△A′B′C′(A和A′,B和B′,C和C′分别是对应顶点),直线y=x+b经过点A,C′,则点C′的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:

乙校成绩统计表
分数/分
人数/人
70
7
80
90
1
100
8
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知s甲2=135,s乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
相关试题

