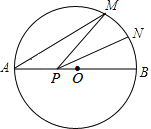
【题目】如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点.若MN=1,则△PMN周长的最小值为( )
A.4 B.5 C.6 D.7
参考答案:
【答案】B
【解析】
试题分析:作N关于AB的对称点N′,连接MN′,NN′,ON′,ON,由两点之间线段最短可知MN′与AB的交点P′即为△PMN周长的最小时的点,根据N是弧MB的中点可知∠A=∠NOB=∠MON=20°,故可得出∠MON′=60°,故△MON′为等边三角形,由此可得出结论.
解:作N关于AB的对称点N′,连接MN′,NN′,ON′,ON.
∵N关于AB的对称点N′,
∴MN′与AB的交点P′即为△PMN周长的最小时的点,
∵N是弧MB的中点,
∴∠A=∠NOB=∠MON=20°,
∴∠MON′=60°,
∴△MON′为等边三角形,
∴MN′=OM=4,
∴△PMN周长的最小值为4+1=5.
故选:B.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)请找出该残片所在圆的圆心O的位置(保留画图痕迹,不必写画法);
(2)若此圆上的三点A、B、C满足AB=AC,BC=3
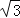 ,且∠ABC=30°,求此圆的半径长.
,且∠ABC=30°,求此圆的半径长.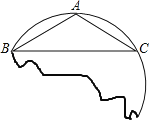
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P是第三象限内的点,且点P到x轴的距离是4,到y轴的距离是3,则点P的坐标是( )
A. (﹣4,-3) B. (4,﹣3) C. (﹣3,-4) D. (3,﹣4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是1260°,这个多边形的边数是( )
A. 6 B. 7 C. 8 D. 9
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的两边长分别为4cm和7cm,第三边长是一元二次方程x2﹣10x+21=0的实数根,则三角形的周长是 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+kx+1=0有两个相等的实数根,则k=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把点(2,﹣3)先向右平移3个单位长度,再向上平移2个单位长度得到的点的坐标是( )
A. (5,﹣1) B. (﹣1,﹣5) C. (5,﹣5) D. (﹣1,﹣1)
相关试题

