搜索
【题目】如图，△ABC中，∠B＝80°，∠C＝40°，
（1）尺规作图：作AC的垂直平分线，交AC于点D，交BC于点E；
（2）连接AE，求证：AB＝AE.
参考答案：
【答案】（1）详情见解析；（2）证明见解析.
【解析】
（1）分别以A、C为圆心，大于
AC为半径画弧，连接弧的交点，交AC于点D，交BC于点E即可；
（2）根据线段垂直平分线的性质得出∠EAC的度数，进一步得出∠BAE的度数，然后根据题意求出∠AEB的度数，进而判断求证即可.
（1）如图所示：
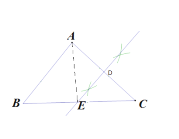
（2）∵DE是线段AC的垂直平分线，
∴AE=EC，
∵∠C＝40°，
∴∠EAC=40°，
又∵∠B＝80°，
∴∠BAC=60°，
∴∠BAE=20°，
∵∠B＝80°，
∴∠AEB=80°，
∴△ABE是等腰三角形，
∴AB＝AE.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，等边△ABC中，BD⊥AC于点D，AD＝3.5cm，点P、Q分别为AB、AD上的两个定点且BP＝AQ＝2cm，若在BD上有一动点E使PE＋QE最短，则PE＋QE的最小值为_____cm
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，A为y轴正半轴上一点，过点A作x轴的平行线，交函数
的图象于B点，交函数
的图象于C，过C作y轴和平行线交BO的延长线于D．（1）如果点A的坐标为（0，2），求线段AB与线段CA的长度之比；
（2）如果点A的坐标为（0，a），求线段AB与线段CA的长度之比；
（3）在（1）条件下，四边形AODC的面积为多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在ABCD中，E是BC的中点，连接AE并延长交DC的延长线于点F．
（1）求证：AB=CF；
（2）连接DE，若AD=2AB，求证：DE⊥AF．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图已知：E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别为C、D．求证：
（1）∠ECD=∠EDC；
（2）OE是CD的垂直平分线．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.
(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在等腰△ABC中，AB＝AC＝3，∠B＝30°，点D在线段BC上运动（点D不与点B、C重合），连接AD，作∠ADE＝30°，DE交线段AC于点E.
（1）D点运动到图1位置时，∠BDA＝75°，则∠EDC＝______，∠DEC＝________；
（2）D点运动到图2位置时，当DC等于多少时，△ABD≌△DCE，请说明理由；
（3）在点D的运动过程中，△ADE的形状也在变化，判断当△ADE是等腰三角形时，∠BDA等于多少度（请直接写出结果）.
相关试题
