【题目】如图,在等腰△ABC中,AB=AC=3,∠B=30°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=30°,DE交线段AC于点E.

(1)D点运动到图1位置时,∠BDA=75°,则∠EDC=______,∠DEC=________;
(2)D点运动到图2位置时,当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状也在变化,判断当△ADE是等腰三角形时,∠BDA等于多少度(请直接写出结果).
参考答案:
【答案】(1)75°,75°;(2)DC=3,理由见解析;(3)当△ADE是等腰三角形时,∠BDA度数为105°或60°.
【解析】
(1)根据三角形内角和与三角形外角等于与其不相邻两内角的和的关系进行求解即可;
(2)根据全等三角形的性质及判定定理综合运用求解即可;
(3)根据△ADE是等腰三角形,分①当AD=AE,②DA=DE,③EA=ED三种情况进行讨论即可.
(1)∵∠BDA=75°,
∴∠ADC=105°,
又∵∠ADE=30°,
∴∠EDC=75°,
∵△ABC是等腰三角形,
∴∠C=∠B=30°,
∴∠DEC=75°,
所以答案为75°,75°;
(2)当DC=3时,△ABD≌△DCE,
∵AB=AC=3,∠B=30°,
∴∠C=30°,
∵CD=CA=3,
∴∠CAD=∠CDA=75°,
∴∠ADB=105°,∠EDC=45°,
∴∠DEC=105°,
∴∠ADB=∠DEC,
在△ABD与△DCE中,
∵∠ADB=∠DEC,AB=DC,∠B=∠C,
∴△ABD≌△DCE;
(3)①当AD=AE时,∠ADE=30°,
∴∠AED=∠ADE=30°,∠DAE=120°,
∵∠BAC=120°,D不与B、C重合,
∴AD≠AE;
②当DA=DE时,∠ADE=30°,
∴∠DAE=∠DEA=75°,
∴∠BDA=∠DEC=180°-∠AED=105°;
③当EA=ED时,∠ADE=30°,
∴∠EAD=∠EDA=30°,
∴∠AED=180°-∠EAD-∠EDA=120°,
∴∠BDA=∠DEC=60°.
综上所述,当△ADE是等腰三角形时,∠BDA度数为105°或60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠B=80°,∠C=40°,
(1)尺规作图:作AC的垂直平分线,交AC于点D,交BC于点E;
(2)连接AE,求证:AB=AE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图已知:E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.求证:

(1)∠ECD=∠EDC;
(2)OE是CD的垂直平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.

(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学问题:计算
 (其中m,n都是正整数,且m≥2,n≥1).
(其中m,n都是正整数,且m≥2,n≥1).探究问题:为解决上面的数学问题,我们运用数形结合的思想方法,通过不断地分割一个面积为1的正方形,把数量关系和几何图形巧妙地结合起来,并采取一般问题特殊化的策略来进行探究.
探究一:计算
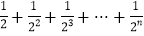 .
.第1次分割,把正方形的面积二等分,其中阴影部分的面积为
 ;
;第2次分割,把上次分割图中空白部分的面积继续二等分,阴影部分的面积之和为
 +
+ ;
;第3次分割,把上次分割图中空白部分的面积继续二等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后二等分,所有阴影部分的面积之和为
 +
+ +
+ +…+
+…+ ,最后空白部分的面积是
,最后空白部分的面积是 .
.根据第n次分割图可得等式:
 +
+ +
+ +…+
+…+ =1﹣
=1﹣ .
.
探究二:计算
 +
+ +
+ +…+
+…+ .
.第1次分割,把正方形的面积三等分,其中阴影部分的面积为
 ;
;第2次分割,把上次分割图中空白部分的面积继续三等分,阴影部分的面积之和为
 +
+ ;
;第3次分割,把上次分割图中空白部分的面积继续三等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后三等分,所有阴影部分的面积之和为
 +
+ +
+ +…+
+…+ ,最后空白部分的面积是
,最后空白部分的面积是 .
.根据第n次分割图可得等式:
 +
+ +
+ +…+
+…+ =1﹣
=1﹣ ,
,两边同除以2,得
 +
+ +
+ +…+
+…+ =
= ﹣
﹣ .
.
探究三:计算
 +
+ +
+ +…+
+…+ .
.(仿照上述方法,只画出第n次分割图,在图上标注阴影部分面积,并写出探究过程)

解决问题:计算
 +
+ +
+ +…+
+…+ .
.(只需画出第n次分割图,在图上标注阴影部分面积,并完成以下填空)
根据第n次分割图可得等式:_________,
所以,
 +
+ +
+ +…+
+…+ =________.
=________.拓广应用:计算
 +
+ +
+ +…+
+…+ .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知△ABC中,AB=BC=1,∠ABC=90°,把一块含30°角的直角三角板DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DE,长直角边为DF),将直角三角板DEF绕D点按逆时针方向旋转.

(1)在图1中,DE交边AB于M,DF交边BC于N,证明:DM=DN;
(2)在这一旋转过程中,直角三角板DEF与△ABC的重叠部分为四边形DMBN,请说明四边形DMBN的面积是否发生变化?若发生变化,请说明是如何变化的?若不发生变化,求出其面积;
(3)继续旋转至如图2的位置,延长AB交DE于M,延长BC交DF于N,DM=DN是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
相关试题

