【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当DE=AE时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.其中正确的是( )

A.②③B.②④C.①③④D.②③④
参考答案:
【答案】D
【解析】
根据角平分线性质求出DE=DF,证△AED≌△AFD,推出AE=AF,再一一判断即可.
解:根据已知条件不能推出OA=OD,∴①错误;
∵AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,
∴DE=DF,∠AED=∠AFD=90°,
在Rt△AED和Rt△AFD中,![]() ,
,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∵AD平分∠BAC,
∴AD⊥EF,∴②正确;
∵∠BAC=90°,∠AED=∠AFD=90°,
∴四边形AEDF是矩形,
∵AE=AF,
∴四边形AEDF是正方形,∴③正确;
∵AE=AF,DE=DF,
∴AE2+DF2=AF2+DE2,∴④正确;
∴②③④正确,
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据“算法”的约定:在数值转换机中,输入或输出的值写在“平行四边形”框内,计算程序(或步骤)写在“长方形”框内,菱形框则用于对结果作出是否符合要求的判定.因此画数值转换机必须注意框图的选择.
(1)如图,当输入数字为1时,数值转换机输出的结果为 ;
(2)嘉悦的爸爸存入1年期的定期储蓄10000元(假定1年期定期储蓄的年利率为4%)到期后本息和(本金和利息的和)自动转存1年期的定期储蓄.请画出数值转换机,并求出转存几次就能使本息和超过11000元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列哪组条件能够判别四边形ABCD是平行四边形?( )

A. AB∥CD,AD=BC B. AB=CD,AD=BC
C. ∠A=∠B,∠C=∠D D. AB=AD,CB=CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,tan∠ABC=
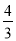 ,∠ACB=45°,AD=8,AD是边BC上的高,垂足为D,BE=4,点M从点B出发沿BC方向以每秒3个单位的速度运动,点N从点E出发,与点M同时同方向以每秒1个单位的速度运动.以MN为边在BC的上方作正方形MNGH.点M到达点C时停止运动,点N也随之停止运动.设运动时间为t(秒)(t>0).
,∠ACB=45°,AD=8,AD是边BC上的高,垂足为D,BE=4,点M从点B出发沿BC方向以每秒3个单位的速度运动,点N从点E出发,与点M同时同方向以每秒1个单位的速度运动.以MN为边在BC的上方作正方形MNGH.点M到达点C时停止运动,点N也随之停止运动.设运动时间为t(秒)(t>0).(1)当t为多少秒时,点H刚好落在线段AB上?
(2)当t为多少秒时,点H刚好落在线段AC上?
(3)设正方形MNGH与Rt△ABC重叠部分的图形的面积为S,求出S关于t的函数关系式并写出自变量t的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
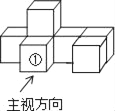
A. 主视图改变,俯视图改变 B. 左视图改变,俯视图改变
C. 俯视图不变,左视图改变 D. 主视图不变,左视图不变
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E为AB边上一点,将△AED沿直线DE翻折,点A落在点P处,且DP⊥BC,垂足为F.
(1)求∠EDP的度数.
(2)过D点作DG⊥DC交AB于G点,且AG=FC,
求证:四边形ABCD为菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】经市场调查,发现进价为40元的某童装每月的销售量y(件)与售价x(元)满足一次函数关系,且相关信息如下:
售价x(元)
60
70
80
90
……
销售量y(件)
280
260
240
220
……
(1)求这个一次函数关系式;
(2)售价为多少元时,当月的利润最大?最大利润是多少?
相关试题

