【题目】为响应市政府“创建国家森林城市”的号召,某小区计划购进A、B两种树苗共17棵,已知A种树苗每棵80元,B种树苗每棵60元.
(1)若购进A、B两种树苗刚好用去1220元,问购进A、B两种树苗各多少棵?
(2)若购买B种树苗的数量少于A种树苗的数量,请你给出一种费用最省的方案,并求出该方案所需费用.
参考答案:
【答案】(1)购进A种树苗10棵,则购进B种树苗7棵 (2)当![]() 时,
时,![]() 元
元
【解析】试题分析:(1)假设购进A种树苗x棵,则购进B种树苗(17-x)棵,利用购进A、B两种树苗刚好用去1220元,结合单价,得出等式方程求解即可;(2)结合(1)的解和购买B种树苗的数量少于A种树苗的数量,可找出方案.
试题解析:
(1)设购进A种树苗x 棵,则购进B种树苗(17-x)棵,根据题意得:
80x+60(17-x )=1220,
80x+1020-60x=1220,
x =10,
∴ 17-x =7.
(2)17-x< x,
解得x >![]() ,
,
购进A、B两种树苗所需费用为80x+60(17-x)=20 x +1020,
则费用最省需x取最小整数9,此时17-x =8,这时所需费用为20×9+1020=1200(元).
答:(1)购进A种树苗10棵,B种树苗7棵;
(2)费用最省方案为:购进A种树苗9棵,B种树苗8棵. 这时所需费用为1200元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算.
(1)(0.25 x -
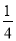 )(0.25 x +0.25);
)(0.25 x +0.25);(2)(x-2 y)(-2y- x)-(3x+4 y)(-3 x +4 y);
(3)(2 a+ b-c-3d) (2 a-b-c+3d);
(4) ( x-2)(16+ x4) (2+x)(4+x2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF.
(1)求证:四边形ABFE是平行四边形;
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】化简.
(1)( x- y)( x+ y) ( x2+ y2) ( x4+ y4)·…·(x16+ y16);
(2)(22+1)(24+1)(28+1)(216+1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育用品商场采购员要到厂家批发购进篮球和排球共100个,付款总额不得超过11815元.已知厂家两种球的批发价和商场两种球的零售价如下表,试解答下列问题:
品名
厂家批发价(元/个)
商场零售价(元/个)
篮球
130
160
排球
100
120
(1)该采购员最多可购进篮球多少个?
(2)若该商场把这100个球全部以零售价售出,为使商场获得的利润不低于2580元,则采购员至少要购篮球多少个?该商场最多可盈利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将代数式x2+10x+17化成(x+a)2+b的形式为( )
A.(x+5)2+8B.(x+5)2﹣8C.(x﹣5)2+10D.(x+5)2﹣10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)填空:点A坐标为 ;抛物线的解析式为 .
(2)在图1中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图2中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?

相关试题

